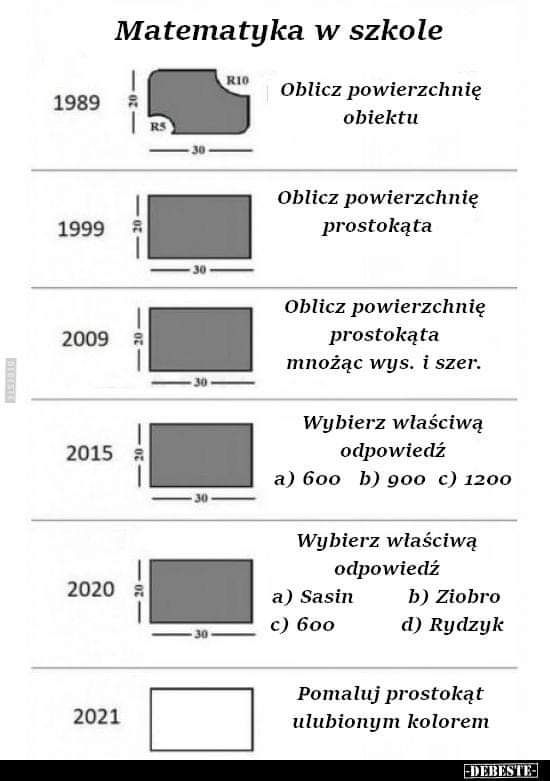
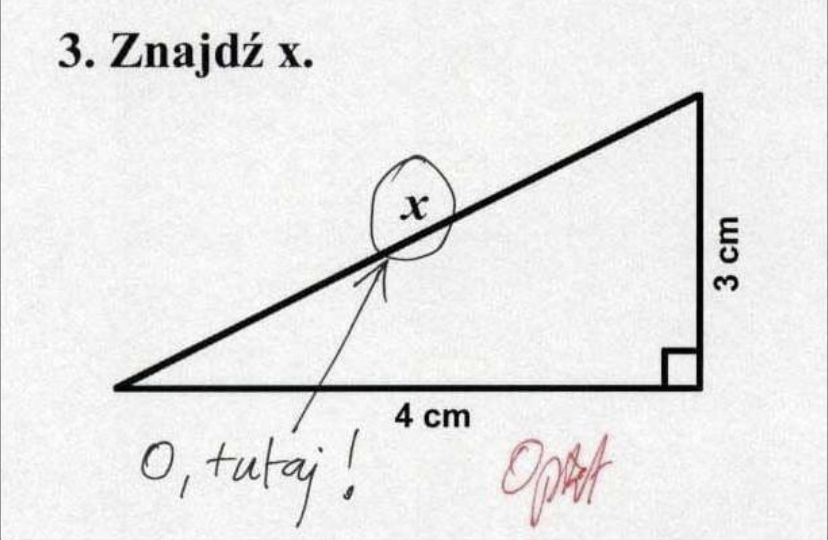
#matematyka
Zaloguj się aby komentować
Zaloguj się aby komentować
Zaloguj się aby komentować
Kilka razy wydawało mi się że w filmach po angielsku słyszę "billion" a tłumaczenie to "miliard". Za pierwszym razem nie miałem pewności czy właśnie nie dostałem wylewu i to pierwszy objaw w postaci częściowej utraty percepcji. Za drugim razem domniemałem po prostu pomyłkę w tłumaczeniu. Ale jak można pomylić się przy takich liczbach - pomyślałem za trzecim.
Można by się spodziewać że każda kolejna wielokrotność 10 powyżej miliona ma podobną nazwę w większości języków zważywszy na giełdy, handel międzynarodowy, prawo bankowe itp.
A tu zonk, surprise mothafuka.
Widocznie tą lekcję angielskiego ominąłem.
Jednak dlaczego te systemy się różnią?
Geneza:
Skala długa (Europa kontynentalna, XVI–XVII w.)
– logiczna, oparta o milion², milion³, milion⁴
Skala krótka (Francja → USA, XIX w.)
– uproszczona do skoków co 10³
Wniosek praktyczny
Polska, nauka, prawo, statystyka → skala długa
Angielski międzynarodowy, finanse, media → skala krótka
Tłumaczenia „jeden do jednego” są błędem, jeśli nie sprawdzi się skali
#ciekawostki #jezykpolski #naukajezykow #jezykangielski #liczby #matematyka

@dolchus ta, jakoś mnie to nie dziwi od kiedy Angole potrafili pogubić przy narzynkach ilość zwoi na cal jak płynęli przez ocean i odpowiednik bsw 1/2 ma 12 zwoi na cal a unc1/2 już 13
anegdotka: bylem ongis na koncercie Jarra i jako przerywnik daje patetyczna przemowe, a ze sluchu jakas tlumaczka przeklada na nasza rodzima mowe na biezaco. no i artysta gada o problemach swiata, cos tam ze "8 billion people living on this world" a tlumaczka przeklada wllasnie jeden do jednego na "8 bilionow ludzi" no i czesc sali w smiech, bo wystarczy wiedziec cokolwiek o tym swiecie zeby dalo do myslenia i skorygowac blad.
mi zawsze to wykreca mozg na lewa strone jak slucham o amerykanskich wydatkach rzadowych, gdzie kwoty wlasnie ida w te miliardy/biliony/trillions i musze sobie przeliczac w glowie, chyba musimy przejsc na notacje wykladnicza
Zaloguj się aby komentować
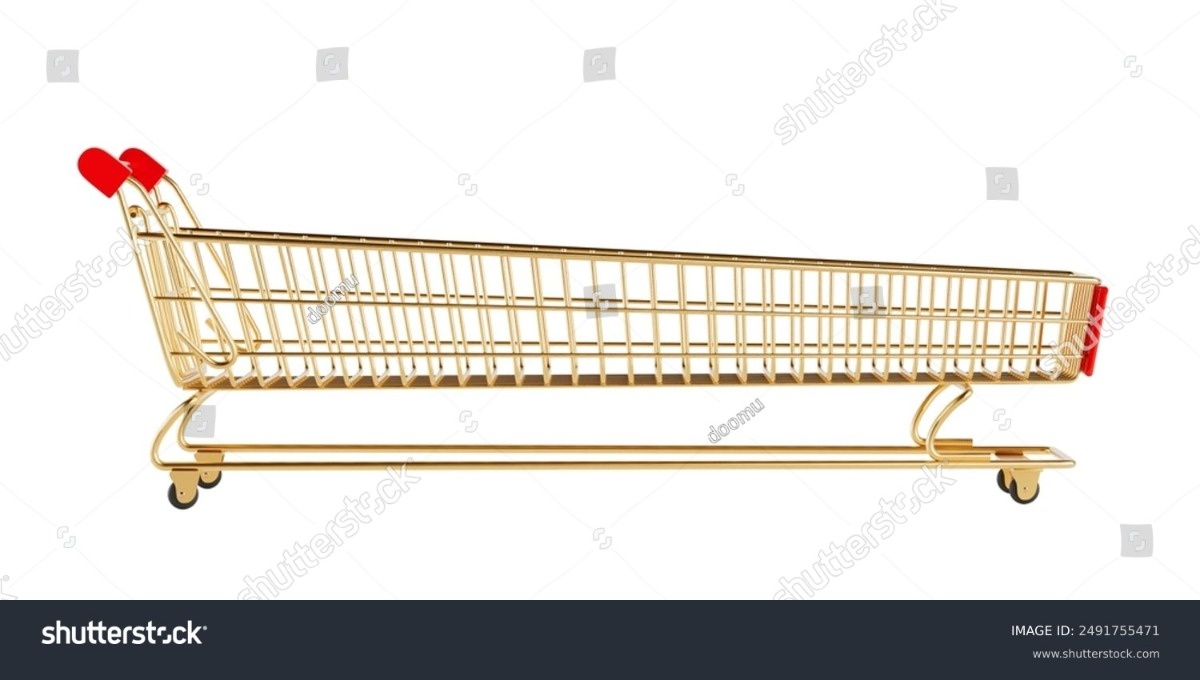
Rozwiązanie wczorajszej Nutrii Matematycznej: wózek ma 3.1 metra długości. Hehe, ciekawe ile osób zwątpiło w swoje umiejętności matematyczne po otrzymaniu poprawnego wyniku bo gdzie takie długie wózki. A są takie długie wózki.
Do zadania można podejść na kilka sposobów. Całość staje się dość łatwa gdy obliczymy sobie ile wynosi "dupka" czyli część wózka nie wsunięta w inny wózek. Skoro rząd 20 wózków ma 8,8 metra a rząd 10 wózków ma 5,8 metra możemy obliczyć długość 10 samych "dupek" zwyczajnie odejmując krótszy rząd od dłuższego, czyli 8,8-5,8 metra = 3 metry. To dzielimy przez 10 i wychodzi nam 0.3 metra. Bierzemy na przykład ten rząd 10 wózków i odejmujemy z niego 9 dupek żeby otrzymać rozwiązanie zadania. 5,8 - 2,7 = 3,1.
#nutriamatematyczna - tag do obserwowania
Przypomnienie zadania:
W dwóch rzędach stoją wózki. Są ściśnięte do granic możliwości tak, że jeden wjeżdża w drugi w sposób jaki przedstawia poniższe zdjęcie.
W jednym z tych rzędów jest 10 wózków. W drugim jest 20 wózków. Każdy poszczególny wózek jest tej samej długości a rzędy mają odpowiednio 5,8 metra i 8,8 metra długości. Ile wynosi długość jednego wózka?
#matematyka #gruparatowaniapoziomu
Zaloguj się aby komentować
W dwóch rzędach stoją wózki. Są ściśnięte do granic możliwości tak, że jeden wjeżdża w drugi w sposób jaki przedstawia poniższe zdjęcie.
W jednym z tych rzędów jest 10 wózków. W drugim jest 20 wózków. Każdy poszczególny wózek jest tej samej długości a rzędy mają odpowiednio 5,8 metra i 8,8 metra długości. Ile wynosi długość jednego wózka?
#nutriamatematyczna - tag do obserwowania
#matematyka #gruparatowaniapoziomu

jak długi jest pojedynczy wózek?
Zaloguj się aby komentować
Rozwiązanie wczorajszej Nutrii Matematycznej.
#nutriamatematyczna - tag do obserwowania
Aby rozwiązać zadanie wystarczy wyeliminować scenariusze, które nie mogą dojść do skutku. Skoro kółka przegrywają ze wszystkimi to nie może być takiego zakończenia rundy, gdzie zostają same kółka bo liczba zawodników się nie spina. Podobnie z kwadratami. Zatem zakładając, że wygrają trójkąty rozgrywamy scenariusz eliminacji odpowiedniej liczby graczy by jak najwięcej kwadratów zostało trójkątami a kółka zostały wyeliminowane. Wtedy odpowiedź to będzie 23. Tylu maksymalnie zawodników mogłoby ukończyć rundę i przejść do kolejnej.
Przypomnienie wczorajszego zadania:
W morderczym turnieju zostało 78 zawodników. Każdy z nich losuje drużynę. Może wylosować trójkąt, kwadracik lub koło.
17 zawodników wylosowało kółko
55 zawodników wylosowało kwadrat
6 zawodników wylosowało trójkąt
Zasady są takie, że zawodnicy błądzą po labiryncie aż dwóch graczy na siebie wpadnie. Gracze mogą na siebie wpadać wielokrotnie aż do zakończenia rundy.
-
zawodnik z trójkątem wpada na zawodnika z kółkiem: kółko jest eliminowane a zawodnik z trójkątem zmienia swój symbol na kwadrat
-
zawodnik z trójkątem wpada na zawodnika z kwadratem: kwadrat jest eliminowany a zawodnik z trójkątem zmienia swój symbol na kółko
-
zawodnik z kwadratem wpada na zawodnika z kółkiem: kółko jest eliminowane a zawodnik z kwadratem zmienia swój symbol na trójkąt
-
dwóch zawodników z tym samym symbolem nic sobie nie robi
W uproszczeniu, przesrane mieć kółko. Gra kończy się gdy wszyscy zawodnicy mają ten sam symbol.
Pytanie, jaka jest najwyższa możliwa liczba graczy, którzy przeszliby do następnej rundy?
#matematyka #ciekawostki

Zaloguj się aby komentować
Dzisiejsza Nutria Matematyczna w klimatach znanego i lubianego serialu koreańskiego Ośmiornicza Gra.
#nutriamatematyczna - tag do obserwowania
W morderczym turnieju zostało 78 zawodników. Każdy z nich losuje drużynę. Może wylosować trójkąt, kwadracik lub koło.
17 zawodników wylosowało kółko
55 zawodników wylosowało kwadrat
6 zawodników wylosowało trójkąt
Zasady są takie, że zawodnicy błądzą po labiryncie aż dwóch graczy na siebie wpadnie. Gracze mogą na siebie wpadać wielokrotnie aż do zakończenia rundy.
-
zawodnik z trójkątem wpada na zawodnika z kółkiem: kółko jest eliminowane a zawodnik z trójkątem zmienia swój symbol na kwadrat
-
zawodnik z trójkątem wpada na zawodnika z kwadratem: kwadrat jest eliminowany a zawodnik z trójkątem zmienia swój symbol na kółko
-
zawodnik z kwadratem wpada na zawodnika z kółkiem: kółko jest eliminowane a zawodnik z kwadratem zmienia swój symbol na trójkąt
-
dwóch zawodników z tym samym symbolem nic sobie nie robi
W uproszczeniu, przesrane mieć kółko. Gra kończy się gdy wszyscy zawodnicy mają ten sam symbol.
Pytanie, jaka jest najwyższa możliwa liczba graczy, którzy przeszliby do następnej rundy?
#matematyka #gruparatowaniapoziomu #ciekawostki

Najwyższa możliwa graczy, która przechodzi do następnej rundy to?
@Rimfire Ok policzone, najpierw trzeba dojść do wniosku kto może wygrać tę zabawę, a następnie policzyć kiedy tego kształtu będzie najwięcej.
Nie jest określone kiedy dunda się kończy. Gracze mogą spotykać się wielokrotnie więc to nie jest warunek zakończenia rundy. Jeśli runda kończy się po 5 minutach a gracze sprytnie będą stali w miejscu to wszyscy przejdą dalej (nie będzie eliminacji).
Zaloguj się aby komentować
Dzisiejsze zadanko takie, że ktoś sobie może pokombinować bez wzoru.
#nutriamatematyczna - niezliczona liczba* użytkowników Hejto kropka pe el obserwuje największy tag sympatyków zadań matematyczno logicznych
Ekipa budowlana ma białe płytki w toalecie wymienić na takie w szachownicę. Majster rozkminił, że skoro płytki układają się we wzór 5x5 to wystarczy kupić tylko 12 czarnych i zostawić 13 białych. Był wtedy jeszcze trzeźwy i w sumie dobrze pomyślał. Zadanie wymiany płytek zlecił świeżakowi, absolwentowi uniwersytetu. W ramach terapii leczenia własnych kompleksów majster postanowił pognębić świeżaka instruując, że ten może wymieniać te płytki tylko w następujący sposób:
-
w dowolnym rzędzie poziomym czy też pionowym może zmienić jednocześnie trzy płytki
-
w jednym ruchu można zmienić tylko trzy płytki znajdujące się obok siebie i w tym samym rzędzie
-
płytka biała zostaje zamieniona w ten sposób na czarną
-
płytka czarna zamieniona zostaje na białą
Okazuje się jednak, że świeżak skończył studia na kierunku matematyka i szybko obliczył w głowie jak wykonać zadanie przy użyciu najmniejszej liczby ruchów (czyli tych zamianek po trzy płytki naraz).
Pytanie: ile ruchów potrzebował świeżak żeby z układu płytek na lewej stronie obrazku przerobić na taki jak na obrazku po prawej?
#matematyka #nauka #ciekawostki #gruparatowaniapoziomu
*niezliczona w przypadku gdy ktoś nie potrafi liczyć do pięciu
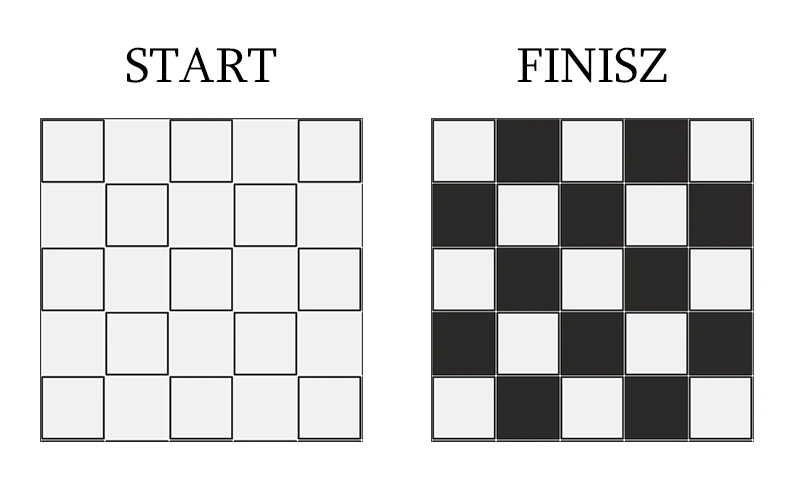
ile zamianek po trzy płytki według instrukcji majstra potrzebował świeżak by wykonać zadanie?
Zaloguj się aby komentować
Rozwiązanie dzisiejszej Nutrii Matematycznej.
Odpowiedź to oczywiście 1.
Przypomnienie zadania:
Rimfire częstuje kolegów cukierasami. W papierowej torbie znajdują się trzy różne typy cukierków. Irysy, michałki oraz szkloki winogronowo-śliwkowe. Jeśli ktoś wyciągnąłby z torby losowo pięć cukierków to co najmniej dwa z nich byłyby szklokami winogronowo-śliwkowymi a co najmniej trzy byłyby tego samego typu. Ile irysów znajduje się w torbie?
Dzisiaj było podchwytliwie ale większość zgadła prawidłowo. By rozwiązać zadanie należy podejść do niego następująco:
-
w torbie są trzy rodzaje cukierków
-
z powyższego wynika, że każdego rodzaju cukierka jest co najmniej jedna sztuka, a szkloków co najmniej dwa.
-
jakiegoś rodzaju cukierków jest trzy sztuki
-
nie może być tak, że pięć losowo wyciągniętych cukierków to będą na pewno dwa szkloki i trzy irysy bądź trzy michałki bo to by oznaczało, że są w torbie tylko trzy rodzaje cukierków
-
z powyższego wynika, że skoro są trzy rodzaje cukierków to fragment o trzech cukierkach tego samego typu również dotyczy szkloków
-
skoro za każdym razem wyciągamy trzy szkloki to pozostają tylko dwa wolne miejsca na cukierki inne niż szkloki
-
jeśli cukierków w torbie byłoby więcej niż pięć to wtedy nie byłoby możliwości, że zawsze wyciągnie się trzy szkloki
Stąd wniosek, że w torbie znajduje się pięć cukierków: trzy szkloki, jeden irys oraz jeden michałek a Rimfire jest spoko ziomkiem, że się dzieli.
#nutriamatematyczna #matematyka

Zaloguj się aby komentować
Dzisiejsza Nutria Matematyczna, czyli największy konkurs matematyczny bez nagród i satysfankcji na Hejto kropka pe el.
Zapraszam do obserwowania tagu #nutriamatematyczna
Rimfire częstuje kolegów cukierasami. W papierowej torbie znajdują się trzy różne typy cukierków. Irysy, michałki oraz szkloki winogronowo-śliwkowe. Jeśli ktoś wyciągnąłby z torby losowo pięć cukierków to co najmniej dwa z nich byłyby szklokami winogronowo-śliwkowymi a co najmniej trzy byłyby tego samego typu. Ile irysów znajduje się w torbie?
#matematyka #gruparatowaniapoziomu

ile irysów może znajdować się w torbie?
Zaloguj się aby komentować
Rozwiązanie dzisiejszej Nutrii Matematycznej.
Odpowiedź to 3.
Przypomnienie zadania:
-
każda linia pionowa zawiera cyfry od 1 do 5
-
każdy linia pozioma zawiera cyfry od 1 do 5
-
w żadnej linii, czy to poziomej czy pionowej, cyfry nie mogą się powtarzać
-
sumy cyfr w polach każdego koloru są sobie równe
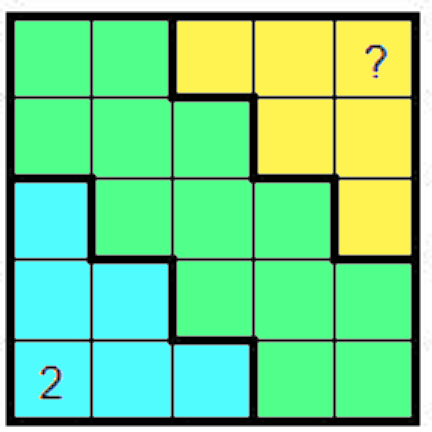
Pytanie: jaka cyfra powinna znajdować się na górnym prawym polu oznaczonym znakiem zapytania?
No to jak się zabrać do zadanka? Otóż następująco.
Po pierwsze, wiemy ile wynosi suma cyfr w każdej linii, bo zawsze są to cyfry 1, 2, 3, 4 i 5. Ta suma wynosi 15.
Po drugie, potrafimy w ten sposób obliczyć ile wynosi suma wszystkich pól. Wynosi ona 15x5, czyli 75.
Po trzecie, wiemy ile wynosi suma cyfr w polach każdego z trzech kolorów gdyż są sobie równe, dlatego musi to być 75 dzielone na trzy, czyli 25.
Po czwarte, znamy tylko jedno pole, znajdujące się w niebieskim zbiorze. Wynosi ono 2. Suma całego niebieskiego zbioru musi wynosić 25. Brakuje pięciu pól z cyframi sumującymi się w 23. Teraz zadanie jest już proste, prawda? Jeśli nadal nie, to dalszą część rozwiązania podaję w komentarzu.
#nutriamatematyczna #matematyka #gruparatowaniapoziomu
Zaloguj się aby komentować
Rozwiązanie wczorajszego odcinka Nutrii Matematycznej, czyli największego konkursu matematycznego bez nagród i satysfankcji na Hejto kropka pe el to: 40 pociągów.
#nutriamatematyczna - niezliczona liczba użytkowników* obserwuje tag, dołącz do nich
Dzisiejsze zadanie z serii trudnych ale przyjemnych. Odłóżcie wzory matematyczne na bok i rozprostujcie zwoje mózgowe. Zaczynamy.
-
każda linia pionowa zawiera cyfry od 1 do 5
-
każdy linia pozioma zawiera cyfry od 1 do 5
-
w żadnej linii, czy to poziomej czy pionowej, cyfry nie mogą się powtarzać
-
sumy cyfr w polach każdego koloru są sobie równe
Pytanie: jaka cyfra powinna znajdować się na górnym prawym polu oznaczonym znakiem zapytania?
Powodzenia!
Jak zwykle, warto zapiorunować wpis dla zasięgu nawet jak nie znasz odpowiedzi.
#matematyka #ciekawostki #gruparatowaniapoziomu
* niezliczona pod warunkiem, że ktoś nie potrafi liczyć
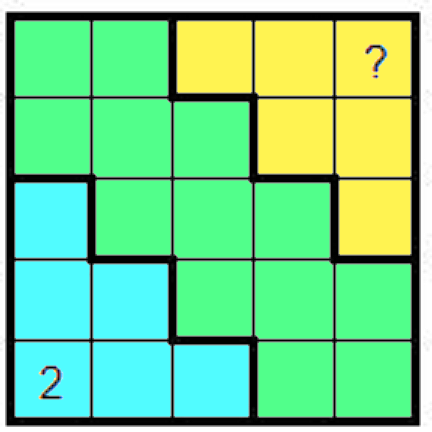
jaka cyfra znajduje się w polu oznaczonym znakiem zapytania?
Zaloguj się aby komentować
Wczoraj było zbyt prosto to dzisiaj trudniej. Przypominam by nie psuć innym zabawy i jakoś zamaskować odpowiedzi w komentarzach oraz by było klawo gdybyście zapiorunowali wpis dla większego zasięgu.
#nutriamatematyczna - oficjalny tag Nutrii Matematycznej, czyli największego matematycznego konkursu bez nagród i satysfakcji na Hejto kropka pe el
Jest 40 pociągów. W sobotę każdy z tych czterdziestu pociągów wykonuje jeden kurs pomiędzy pewnymi dwoma miastami
spośród pięciu miast - Toruń, Bydgoszcz, Kraków, Warszawa i Moszna.
Dziesięć z tych pociągów wykonuje kurs do Torunia albo z Torunia.
Dziesięć z tych pociągów wykonuje kurs do Bydgoszczy albo z Bydgoszczu.
Dziesięć z tych pociągów wykonuje kurs do Krakowa albo z Krakowa.
Dziesięć z tych pociągów wykonuje kurs do Warszawy albo z Warszawy.
Pytanie: ile pociągów wykonuje kurs do Moszny albo z Moszny?
#matematyka #gruparatowaniapoziomu

no ile?
Zaloguj się aby komentować
Dzisiaj zmiana formuły Nutrii Matematycznej i prosiłbym o nie zdradzanie odpowiedzi w komentarzach a zamiast tego wybieramy odpowiedź z ankiety (z kolei procesy obliczania i dyskusja są jak najbardziej mile widziane w komentarzach). Warto zapiorunować wpis dla zasięgu i te sprawy. No to dzisiejsze zadanko.
Eliminacje do mistrzostw świata w piłce nożnej. Zwycięzca meczu otrzymuje 3 punkty, przy remisie każda drużyna otrzymuje po punkcie a pokonana drużyna no cóż 0 punktów.
Polska trafia po raz kolejny do ciężkiej grupy, która prezentuje się następująco.
NAMIBIA
CHINY
TANZANIA
POLSKA
Każda z drużyn rozegrała po jednym meczu z pozostałymi trzema. Innymi słowy trzy mecze po jednym
z każdą inną. Po zakończeniu turnieju Chiny zdobyły 7 punktów. Namibia i Tanzania po 4 punkty. Ile punktów zdobyła Polska?
#nutriamatematyczna - coraz więcej obserwujących najbardziej prestiżowy tag matematyczny dla matematycznych wyjadaczy matematycznych zadanek na Hejto kropka pe el
#matematyka #gruparatowaniapoziomu #pilkanozna

Ile punktów zdobyła Polska?
Chiny musiały wygrać 2 mecze i mieć remis. Namibia i Tanzania wygraną i remis.
Możliwą opcją jest że Chiny wygrały z Namibią i Tanzanią, i zremisowały z Polską. Namibia i Tanzania wygrały z Polską, remis między sobą. Wtedy Polska ma 1pkt.
Polska mogła też zremisować z Namibią lub Tanzanią, a wtedy druga z tych dwóch (ta co nie zremisowała z Polską) zremisowała z Chinami.
Nie ma tu innych możliwości :P
Można byłoby zadać zagadkę typu 3 drużyny w grupie mają 6pkt, czy i jak to jest możliwe?
@Rimfire mamy 6 meczów, Chiny musiały wygrać 2, pozostali po 1, i mamy 2 remisy, więc wszystko juz wiadomo
Zaloguj się aby komentować
Dzisiejsze zadanko dużo prostsze od wczorajszego. Rimfire smaży placki ziemniaczane. Wychodzą mu za⁎⁎⁎⁎ste ale nie o to chodzi. Razem usmażył 6 placków. Każdy smażył na patelni pojedynczo. Numerowane są od 1 do 6 (od najwcześniej usmażonego do najpóźniej usmażonego). Co chwilę do kuchni wpadał dzieciak, który zjadał najbardziej gorący placek. W jakiej kolejności nie mógł zjeść placków i jak to obliczyłeś?
A 1, 2, 3, 4, 5, 6
B 1, 2, 5, 4, 3, 6
C 3, 2, 5, 4, 6, 1
D 4, 5, 6, 2, 3, 1
E 6, 5, 4, 3, 2, 1
#nutriamatematyczna #matematyka #gruparatowaniapoziomu

Zaloguj się aby komentować
Rozwiązanie dzisiejszej Nutrii Matematycznej. Jako pierwszy zadanie rozgryzł (hehe) znany i lubiany @maximilianan
Przypominamy zadanie. Marysia ma dwójkę dzieci. Mówi, że jedno z nich to chłopiec urodzony we wtorek. Jakie jest prawdopodobieństwo, że drugie dziecko jest dziewczynką?
Tutaj pojawiło się dużo różnych teorii i niedopowiedzeń. Rozwiązanie jest prostsze niż się może wydawać początkowo. Pamiętajmy, że to jest Nutria Matematyczna. Tutaj rozwiązania często okazują się bardzo proste ale trzeba na nie wpaść.
Zatem, jak się do tego zabrać? Dostajemy dwie informacje. Jedno z dzieci Marysi jest chłopcem, urodzonym w konkretnym dniu.
Najpierw obliczamy ile jest różnych możliwości na podstawie dwóch płci i siedmiu dni.
7 dni gdzie dziewczynka urodziła się po chłopcu
7 dni gdzie dziewczynka urodziła się przed chłopcem
Jest tylko 14 możliwości, w których urodziła się dziewczynka, a nazwa dnia to nie ma znaczenia.
Natomiast nie ma możliwości by drugi chłopiec urodził się w tym samym dniu bo wtedy by nie mogło być "jeden z nich jest urodzony we wtorek" tylko dwóch.
Pytanie było o procent jaki stanowi prawdopodobieństwo, że drugie dziecko jest dziewczynką, który obliczamy dzieląc 14 (liczba możliwości dnia, w których mogła urodzić się dziewczynka) przez 27 (liczba możliwości dnia w którym mogła się urodzić albo dziewczynka albo drugi chłopiec). Czyli 51,8%
#nutriamatematyczna #matematyka #gruparatowaniapoziomu

Nie rozumiem dlaczego bierzemy 14 dni. Zrozumiałe jest, że we wtorek mógł się urodzić tylko jeden chłopiec, wynika to z informacji od matki, tak jak napisałeś. Dziewczynka mogła się urodzić we wtorek. Okej. Tylko skąd 14 dni? Dlaczego 7 w przód i 7 w tył?
Na podstawie tego, że tydzień ma 7 dni, to powiedziałbym że w ciągu tygodnia jest 7 dni-możliwości na urodzenie dziewczynki i 6 na urodzenie chłopca (wypada nam wtorek bo inaczej Marysia byłaby kłamczuszkiem), a to daje 13 możliwości. Dziewczynka mogła urodzić się w dowolny dzień i to nie jest sprzeczne z informacjami które dostaliśmy. A wtedy 7/13 daje nam 53,85%. Kolejność urodzenia dzieci nie ma znaczenia. Skąd tam się wzięło 27?
@ZohanTSW bo dzieci jest dwójka i nie wiesz które urodziło się wcześniej. Zatem robisz opcje dla tego chłopaka co się urodził we wtorek jako młodsze dziecko i opcje jako tego wtorkowego chłopaka jako starsze dziecko. Dodajesz je wszystkie do puli możliwości. Możliwości typu starszy brat i młodsza siostra, młodszy brat i starsza siostra oraz dwóch braci (ci mają 2 opcje gdzie dzieciak wspomniany w zadaniu jest albo starszy albo młodszy). Cztery razy 7 to jest 28. Ale nie może być dwóch braci urodzonych tego samego dnia tego konkretnego wtorku. Zatem 28-1. Opcji z siostrą jest tylko 14. Czyli 14 dzielisz przez 27 i Ci wychodzi wynik. Proste.
@bori @Paulie @mahoney @pszemek bo zaplusowaliście Colegę powyżej to zakładam, że też nie skumaliście. Powyżej rozpisałem dokładne wyjaśnionko co jak i dlaczego. Teraz kumata?
Zaloguj się aby komentować
Dzień dobry, Nutrie! Skoro już się pobawiliśmy z matematycznymi zagwozdkami i prostymi zadankami pora na coś dla prawdziwych wyjadaczy matematycznych.
Marysi urodził się syn we wtorek.
To jedno z jej dwojga dzieci.
Jakie jest prawdopodobieństwo, że drugie dziecko to dziewczynka?
Jeden z panów mówi, że 66,6% a drugi 51,8%
Który z nich ma rację i jak to obliczyć?
Ja już wiem. A Ty? Czy jesteś w stanie rozwiązać zagadkę w dzisiejszym wydaniu Nutrii Matematycznej?
Do dzieła, mądre głowy!
#matematyka #nutriamatematyczna #gruparatowaniapoziomu

@Rimfire 40%. Albo jest to dziewczynka albo nie jest to dziewczynka. 50/50, ale dwadzieścia procent pobiera tutaj kasa, ruda Grażyna ty jesteś ekstra klasa
@Rimfire
Nie cierpię takich zadań, bo wynik zależy od tego, jakie założenia przyjmiesz. I jeśli przyjmiesz inne niż twórca zadania to otrzymasz inny wynik.
Założenia twórcy powinny być więc podane wprost, bez zgadywania.
A brzmią one:
-
Zadanie jest czysto probabilistyczne. Nie bierzemy pod uwagę uwarunkowań ekonomicznych, biologicznych czy statystycznych.
-
Zakładamy, że w zadaniu chodzi o rodzaje możliwych zdarzeń dla różnych dni tygodnia. A nie np. miesiąca czy roku. Tak, wtorek to dzień tygodnia, ale przyjęcie, że jest to również ograniczenie do dni tygodnia to właśnie założenie.
-
Pełny temat zadania zakłada zatem prawdopodobieństwo wystąpienia dwóch różnych i niepowiązanych zdarzeń w odniesieniu do dni tygodnia.
A ja np. tak właśnie nie myślę. Więc wkurzają mnie zadania, w których dobrowolnie zamykasz się w takim ciasnym pokoiku i wyrzucasz klucz.
Bo Mary to może być Maria, jej chłopiec może mieć na imię Jezus, i cuda mogą się zdarzyć.
Albo drugie dziecko mogłoby mieć chromosomy XXY i mieć zespół Klinefeltera.
Albo drugie dziecko mogło być adoptowane.
Etc.
Zaloguj się aby komentować
Dawno nie było nic pod tagiem #nutriamatematyczna
No to szybkie i przyjemne zadanko na rozprostowanie zwojów mózgowych.
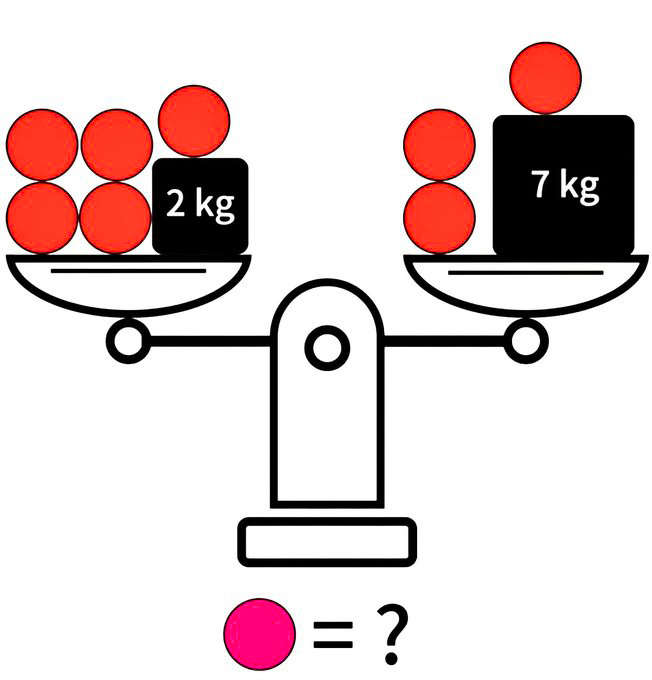
Na obrazku jest waga. Na każdej szali postawiono odważnik. Na lewej jest to odważnik ważący 2 kilogramy a na prawej odważnik ważący 7 kilogramów.
Po dodaniu czerwonych kulek szale wyrównały się. Każda z kulek położonych na szali waży tyle samo. Kulka koloru magenta waży dwukrotnie tyle ile kulka czerwona.
Pytanie: ile waży kulka przedstawiona na dole obrazka?
#matematyka
Zaloguj się aby komentować
Orbity keplerowskie są przekrojami stożka (a w przypadkach zamkniętych oczywiście elipsami)
Dałem #heheszki i z obrazka chyba widać czemu
Ale poza beką, to dosyć ciekawa i nieco głębsza historia z dodatkowymi ciekawostkami. Tutaj jest nieco szczegółowiej: https://math.ucr.edu/home/baez/gravitational.html .
Keplerowskie orbity zamknięte są sekcjami stożka z powodu prawa odwróconego kwadratu. Ale co mniej oczywiste, orbity takie mają symetrię SO(4) - czyli cztero, a nie trójwymiarową. A wynika to z tego, że prawo odwróconego kwadratu ma więcej symetrii, niż przestrzeń, w której się je stosuje. Sama grupa ma de facto 6 stopni swoboody, symetrii (można rzec, że wymiarów), ale jest opisywalna w 4 wymiarach, bo dodaje jedynie wektor pędu. Wiem, że nie chcialiście tego wiedzieć, ale nie dałem Wam wyboru
https://xkcd.com/3189/
#okazjonalnexkcd #matematyka #fizyka #nauka #ciekawostki #heheszki
A o elipsach i problemie z wyznaczeniem ich dokładnej długości już pisałem (w skrócie, nie da się, napewno). Ale skoro ciekawostka to Ramanujan (taki Hindus, co robił outsourcing w matematyce, zanim to stało się modne) dał dobre przybliżenie:
L ≈ π(a + b)(1 + 3h/(10 + √(4 - 3h))) przy h = (a - b)²/(a + b)²
Zaloguj się aby komentować