119 684 270 - 250 = 119 684 020
Byłem ciekawy, czy uda mi się zjeść ćwierć kilo samego twarogu bez niczego innego.
Udało się.
#pletwalztwarogu
Wpis dodany za pomocą https://hejtostats.pl . @Marvin certified! #statsbymarvin
@spalona_zarowka o kurcze, szacunek ja nie daję rady
ciekawe kto jest producentem tego twojego klinka ze zdjęcia bo u mnie jest mlekowita i mam inne staty w tabelce wartości odżywczych
@owczareknietrzymryjski Wyprodukowano przez POLMLEK Raciąż Sp. z o.o. A kupiono w krakowskiej biedronce
Zaloguj się aby komentować
Hej,
w ramach jesiennych wyzwań dostałem zestaw:
Namaluj dowolną techniką jesienny obraz
Wybierz się dowolnym środkiem transportu do pobliskiego miasta, w którym dawno nie byłeś i pokaż go z najciekawszej strony
Napisz list do samego siebie, który otworzysz za rok o tej porze
U mnie wybór padł na pierwszy punkt z małym twistem. Jako, że do duszy artystycznej mi daleko i byłoby to widać, to stwierdziłem, że podzielę się chociaż czymś ciekawym
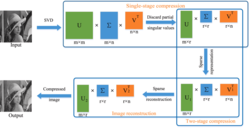
Na załączonych obrazkach widać obraz "namalowany" techniką kompresji a następnie dekompresji zdjęcia metodą SVD.
Górne zdjęcie jest oryginałem, dolne po cyklu kompresja -> dekompresja. Oryginalny rozmiar zdjęcia (gdyby zapisać je wprost, piksel po pikselu, z trzema wartościami R, G i B) to 12712.50 KiB, a rozmiar po kompresji to 4372.81 KiB, co stanowi 34.40% rozmiaru oryginalnego. Na następnych zdjęciach widać poszczególne kanały R, G i B oraz to w jaki sposób zostały skompresowane przez algorytm.
Metoda kompresji SVD jest de facto metodą kompresji macierzy a nie obrazu, z tego względu plik wejściowy należy wstępnie przetworzyć rozbijając go na 3 kolory składowe. Tak uzyskane trzy macierze możemy skompresować każdą z osobna, przeprowadzając jej rozkład zgodnie ze wzorem z ostatniego zdjęcia. Sam rozkład SVD jednak nie pomaga nam przy kompresji, ponieważ jest to matematycznie równość, a zamiast przechować NxM danych, mamy teraz MxM (macierz U) + MxN (macierz Σ) + NxN (macierz Vᵀ). Na szczęście jednak wartości na przekątnej macierzy Σ spadają na tyle szybko, że możemy obciąć wszystkie trzy macierze zachowując tylko r najważniejszych wierszy i/lub kolumn. Właśnie w tym momencie następuje stratna kompresja obrazu (nie jesteśmy potem w stanie idealnie odtworzyć tego co było na wejściu).
Algorytm, który wygenerował poniższe zdjęcia dodatkowo najpierw oblicza rozkład przy użyciu SVD, a następnie decyduje czy nie byłoby korzystne rozbicie macierzy rekurencyjnie na cztery mniejsze, co podnosi skuteczność kompresji w momencie gdy dana macierz jest jednolita w lokalnym obszarze (wtedy brak jest rozbicia na fragmenty i mamy mniej wartości do przechowania) lub zróżnicowana pod względem wartości (wtedy następuje rozbicie aby możliwe było dokładniejsze zachowanie cech obrazu). Sposób tego podziału jest widoczny na czarnobiałych diagramach. Pokazuje to rozkład i udział każdego z kolorów w końcowym obrazie.
W efekcie przechowujemy trzy drzewa dla każdego koloru, gdzie w liściach (pojedyncza komórka na czarnobiałym podziale) znajdziemy informację o tym który konkretnie fragment obrazu jest przechowywany w danym liściu oraz macierze U, Σ i Vᵀ służące do odtworzenia tego właśnie fragmentu. W celu dekompresji tak zachowanego obrazu wystarczy odpowiednio przemnożyć wartości U, Σ i Vᵀ aby dzięki temu otrzymać rekonstrukcję wartości wejściowych i zapisać je w odpowiednim fragmencie buforu.
Więcej o tym można poczytać tutaj . Z tej strony pochodzi też obrazek objaśniający kroki kompresji obrazu.
P.S.
Rykoszetem "wykonałem" również zadanie drugie, bo zdjęcie (choć nie moje, dlatego odznaczam tylko punkt pierwszy :P), przedstawia jesienny park zdrojowy w Busku-Zdroju, moją rodzinną okolicę
#jesiennewyzwania #nauka #matematyka
@spalona_zarowka sorry, ale hejto tak kompresuje obrazki, że nie widać różnicy xD
@Felonious_Gru tego się bałem 😆 Chciałem tak dobrać paramtery żeby ładnie było widać różny rozkład poszczególnych kolorów, jak będę miał moment to przygotuję wizualizację w której lepiej widać artefakty kompresji. Na ten moment możesz się przyjrzeć liściom na drzewach w samym centrum zdjęcia, tam widać charakterystyczne pionowe i poziome rozmazania
@spalona_zarowka jak się mocno powiększy yo cos tam widać.
Sprobuj na imgur może
Hmm... Bardzo ciekawe, nic nie zrozumiałem.
@sireplama to bardzo niedobrze bo znaczy to tyle że źle opisałem proces
W takiej prostej analogii polega to na rozbiciu zapisu obrazu na pojedyncze liczby a potem rozbiciu tych liczb w sposób który zajmuje mniej miejsca w komputerze, np. 774367 to w przybliżeniu 770000 = 77*10⁴ (więc zamiast pamiętać 6 cyfr pamiętamy tylko trzy, bo 77 i 4 jako potęgę do której należy podnieść 10 jeśli przyjmiemy konwencję że zawsze zapisujemy kompresję w tej postaci) i w zależności od tego jak duże przybliżenie założymy, tak dużą kompresję otrzymamy
Tyle tylko że mnożymy macierze a nie liczby
Taki amigowy Bitplane
Zaloguj się aby komentować
Cześć,
razem z dziewczyną wybieramy się niedługo do Albanii w okolice Durres na tydzień. Mamy już załatwione organizowane wycieczki do Berat, safari po Golem i rejs na Sazan. Mamy oprócz tego jeszcze w sumie jeden wolny dzień, polecacie gdzieś się udać? Myślałem o wypadzie do Kruja ale nie wiem czy warto bez przewodnika. I druga sprawa, ile pieniędzy myślicie warto przeznaczyć na "wolne wydatki"? W stylu obiad, pamiątki, jakieś busy itp. Szacowałem na początku około 350 euro, ale nie chcę wziąć za mało. Trzy obiady odpadają bo są w cenie wycieczek.
Dzięki z góry za wszystkie rady i sugestie!
@spalona_zarowka nie wiem czy oni dalej mają problem ze zmianą waluty czy próbują oszukiwać w głupi sposób ale czasem potrafią rzucić cenę 10x za dużą i udawać, że jest wszystko w porządku
Zaloguj się aby komentować
ruszamy i tutaj, może uda nam się dobierać 😎
2zł znalezione przed przystankiem w drodze na kolosa, życzcie mi szczęścia 😋😇
zasady:
zaczynamy od 100 000 000 groszy
odejmujemy znaleziony nominał w groszach
chwalimy się
do uzbierania pozostało:
100 000 000 - 200 = 99 999 800
#stomilionowschylenpogrosz
Zaloguj się aby komentować
