Hej,

w ramach jesiennych wyzwań dostałem zestaw:

• Namaluj dowolną techniką jesienny obraz

• Wybierz się dowolnym środkiem transportu do pobliskiego miasta, w którym dawno nie byłeś i pokaż go z najciekawszej strony

• Napisz list do samego siebie, który otworzysz za rok o tej porze

U mnie wybór padł na pierwszy punkt z małym twistem. Jako, że do duszy artystycznej mi daleko i byłoby to widać, to stwierdziłem, że podzielę się chociaż czymś ciekawym

Na załączonych obrazkach widać obraz "namalowany" techniką kompresji a następnie dekompresji zdjęcia metodą SVD.

Górne zdjęcie jest oryginałem, dolne po cyklu kompresja -> dekompresja. Oryginalny rozmiar zdjęcia (gdyby zapisać je wprost, piksel po pikselu, z trzema wartościami R, G i B) to 12712.50 KiB, a rozmiar po kompresji to 4372.81 KiB, co stanowi 34.40% rozmiaru oryginalnego. Na następnych zdjęciach widać poszczególne kanały R, G i B oraz to w jaki sposób zostały skompresowane przez algorytm.

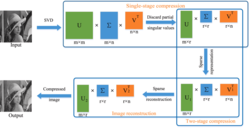
Metoda kompresji SVD jest de facto metodą kompresji macierzy a nie obrazu, z tego względu plik wejściowy należy wstępnie przetworzyć rozbijając go na 3 kolory składowe. Tak uzyskane trzy macierze możemy skompresować każdą z osobna, przeprowadzając jej rozkład zgodnie ze wzorem z ostatniego zdjęcia. Sam rozkład SVD jednak nie pomaga nam przy kompresji, ponieważ jest to matematycznie równość, a zamiast przechować NxM danych, mamy teraz MxM (macierz U) + MxN (macierz Σ) + NxN (macierz Vᵀ). Na szczęście jednak wartości na przekątnej macierzy Σ spadają na tyle szybko, że możemy obciąć wszystkie trzy macierze zachowując tylko r najważniejszych wierszy i/lub kolumn. Właśnie w tym momencie następuje stratna kompresja obrazu (nie jesteśmy potem w stanie idealnie odtworzyć tego co było na wejściu).

Algorytm, który wygenerował poniższe zdjęcia dodatkowo najpierw oblicza rozkład przy użyciu SVD, a następnie decyduje czy nie byłoby korzystne rozbicie macierzy rekurencyjnie na cztery mniejsze, co podnosi skuteczność kompresji w momencie gdy dana macierz jest jednolita w lokalnym obszarze (wtedy brak jest rozbicia na fragmenty i mamy mniej wartości do przechowania) lub zróżnicowana pod względem wartości (wtedy następuje rozbicie aby możliwe było dokładniejsze zachowanie cech obrazu). Sposób tego podziału jest widoczny na czarnobiałych diagramach. Pokazuje to rozkład i udział każdego z kolorów w końcowym obrazie.

W efekcie przechowujemy trzy drzewa dla każdego koloru, gdzie w liściach (pojedyncza komórka na czarnobiałym podziale) znajdziemy informację o tym który konkretnie fragment obrazu jest przechowywany w danym liściu oraz macierze U, Σ i Vᵀ służące do odtworzenia tego właśnie fragmentu. W celu dekompresji tak zachowanego obrazu wystarczy odpowiednio przemnożyć wartości U, Σ i Vᵀ aby dzięki temu otrzymać rekonstrukcję wartości wejściowych i zapisać je w odpowiednim fragmencie buforu.

Więcej o tym można poczytać tutaj. Z tej strony pochodzi też obrazek objaśniający kroki kompresji obrazu.

P.S.

Rykoszetem "wykonałem" również zadanie drugie, bo zdjęcie (choć nie moje, dlatego odznaczam tylko punkt pierwszy :P), przedstawia jesienny park zdrojowy w Busku-Zdroju, moją rodzinną okolicę

#jesiennewyzwania #nauka #matematyka