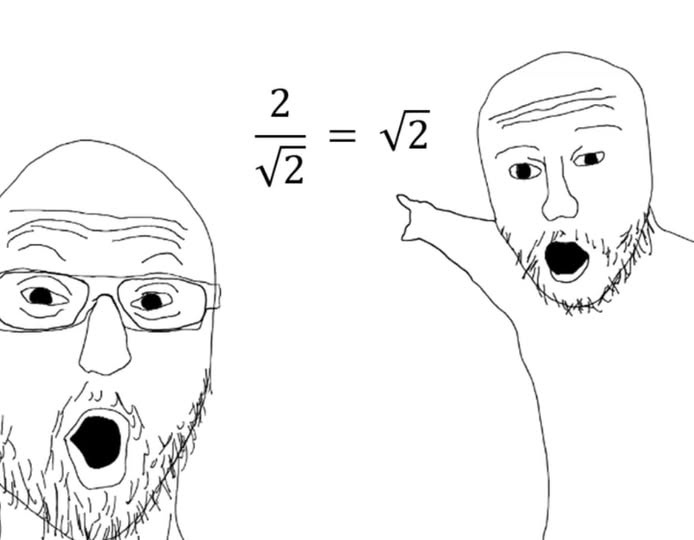#matematyka
@entropy_ dla ciekawych: Historyjka z Gaussem miała wyglądać tak, że nauczyciel matematyki chcąc odpocząć kazał policzyć klasie sumę liczb naturalnych od 1 do 100. Młody Gauss zauważył, że wystarczy dodać 1 i 100, a potem 2 i 99, a potem... i tak ileś razy i uzyskał wynik w kilkanaście sekund xd
@entropy_ i to jeszcze policzone na kalkulatorze xD
#pompujwpoprzekziemi
Zaloguj się aby komentować

Twierdzenia Gödla obala najważniejszy mit AI. AI nie będzie świadoma | Roger Penrose (Nobel 2020)
Czy sztuczna inteligencja może być i czy kiedykolwiek będzie świadoma? Czy powstanie silna AI, która zastąpi człowieka na wielu płaszczyznach? O tych i wielu innych zagadnieniach z dziedziny sztucznej inteligencji mówi Sir Roger Penrose - jeden z największych umysłów naszych czasów. Zapraszamy na...
Dowód, że e^(iπ)= -1
Wygenerowany w 100% przez AI. Jedyne co ręcznie zrobiłem to wrzuciłem na streamable i napisałem ten post xDDDD
Prompt:
NEW ANIMATION: Using MANIM visualize proof that e^ipi=-1
Wygenerowany kod ruszył od strzała xDDD
#matematyka #ai #chatgpt #sztucznainteligencja
@entropy_ jest animacja, a gdzie dowód?
Zaloguj się aby komentować
Dobra, rzucamy kostką d6 raz, czy d12 dwa razy? Co da większe prawdopodobieństwo otrzymania przynajmniej raz cyferki 1, a może prawdopodobieństwo jest takie samo i to bez znaczenia? XD
------------------
#pytanie #memy #matematyka
@entropy_ bo lubisz takie zabawy. xd

Przyfarciłem ;d teraz poproszę mojego miliona.

Wg mnie prawdopodobieństwo jest takie same. W przypadku d12 szansy nie mnożymy, bo nie potrzebujemy 2 rzutów, żeby spełnić warunek.
Więc d6 = 1/6
D12 = 1/12 + 1/12 = 1/6
TL;DR Czerwona daje minimalnie lepsze szanse.
O ile prawdopodobieństwo przy kostce czerwonej łatwo wyliczyć, to obliczenia jak przy niebieskiej kostce mogą być podchwytliwe. Takie przpypadki, gdy coś może udać się przy pierwszej lub drugiej próbie, łatwiej rozpatrywać przez zaprzeczenie - jaka jest szansa że nie wypadnie za pierwszym ani drugim razem?
Są tylko dwie opcje - uda się albo się nie uda. Szansa powodzenia i niepowodzenia sumują się więc do 1 (albo 100%). Szansa wyrzucenia czegoś innego niż 1 to w przypadku pierwszej 5/6, a w przypadku drugiej 11/12 za każdym razem, czyli 11/12 * 11/12, lub 121/144.
Po sprowadzeniu do wspólnego mianownika daje to 120/144 w przypadku czerwonej i 121/144 w przypadku niebiejskiej. Z tego wynika że szansa powodzenia to odpowiednio 24/144 i 23/144 dla kostki 6 i 12-stronnej.
Zaloguj się aby komentować
Ciąg Fibonacciego jest niedorzecznie dobrym przelicznikiem Mil na Kilometry
#ciekawostki #matematyka

"Ciąg Fibonacciego"
@entropy_ Nie będę ciągnął żadnemu fiboczemu zboczuchu!
@entropy_

@entropy_ Złota liczba - około 1.618. Jeden mila - około 1.6093 kilometra. Przypadek? Nie sądze!
Zaloguj się aby komentować
#matematyka
Rachunek różniczkowy jest czymś niesamowitym, zwłaszcza dla fizyków i inżynierów.
Jeżeli chcemy wiedzieć jak się zachowuje pewien obiekt, to mamy 2 podstawowe rozwiązania:
-Przeanalizować to jak dowolnej chwili zachowuje się obiekt
-Przeanalizować jak zmienił się obiekt od ostatniego pomiaru, wiedząc gdzie był wcześniej
Porównując to do jazdy samochodem żeby wiedzieć jaką odległość pokonaliśmy:
-Opcja pierwsza to zaplanowanie swojej trasy przejazdu co do sekundy
-Opcja druga to patrzenie na prędkościomierz, i liczenie w głowie. Sekundę temu byłem 200m od domu, w ciągu sekundy wg prędkościomerza pokonałem 50 metrów, więc teraz znajduje sie 250m od domu
-Opcjonalnie jest jeszcze GPS, ale tę opcje pomijamy XD
Opcja pierwsza, momentami jest po prostu przejebanie trudna, albo wprost niemożliwa (nie zaplanujemy przecież że w trasie po 766 sekundach natrafimy na korek w którym będziemy stać dokładnie 166 sekund).
Opcja druga daje przybliżone rezultaty, ale im częściej będziemy dokonywać pomiarów tym dokładniejszą wartość otrzymamy.
Tutaj mamy przykład. Załóżmy że mamy wachadło (np. ciężarek na sznurku), i chcemy wiedzieć z jaką prędkością się porusza w danym momencie (np. mamy ten dźwig z kulą do burzenia budynków, i znając masę kuli chcemy policzyć z jaką siłą kula uderzy w budynek).
Policzenie tego do dostania jawnej postaci funkcji (czyli prędkość 5 sekund po rozpoczęciu opadania) jest po prostu przesrane, ale możemy łatwo zrobić dokładną symulację. Mądre głowy wyznaczają jak zmienia się prędkość kuli.
To z jaką siłą przyspiesza, jest zależne od siły grawitacji, długości wachadła, oraz kąta od jakiego zaczynamy (wachadło które zaczyna bez rozbujania nie ruszy z miejsca, a wachadło które startuje pod kątem 90 stopni będzie się poruszać szybko).
No więc wklepujemy do excela jaką mamy siłę grawitacji, początkowe przyspieszenie wachadła (jeżeli zakładamy że od początku jest w ruchu), początkowe ułożenie, i z pomocą zaledwie kilku kolumn możemy zobaczyć jak zmienia się prędkość. Do tego dodajemy że przyspieszamy coraz wolniej, wraz ze wzrostem oporu powietrza (tu oznaczone literą mu).
Mamy 3 stałe liczby które mówią nam o tym "w jakim środowisku uruchamiamy układ", i 3 zmienne. Przyspieszenie (oznaczone przez ''), prędkość (oznaczoną przez '), oraz aktualną pozycje (brak ').
Z pomocą kilku banalnych reguł, możemy zapisać zarąbiście skomplikowane równanie (często niemożliwe do znalezienia), tak żeby dostać wykres który i tak nam powie jak się dany obiekt zachowuje
może dobry będzie tag #gruparatowaniapoziomu


wsm dałem zły tytuł wykresu, bo to nie jest prędkość tylko kąt pod jakim obecnie jest wachadło, ale c⁎⁎j, już wpisane XD
@redve z matmy jestem tępy to się przypieprzę o wahadło.
@redve Pochodną predkosci w czasie jest przyśpieszenie, a pochodną przyspieszenia jest zryw, a pochodną zrywu jest udar. I co z tego wynika? Nie wiem
Zaloguj się aby komentować
Ludzie mi sie dziwią że interesuje sie #matematyka
wielu osobom matematyka kojarzy się ze sprawdzianami ze szkoły, oraz wykuwaniem na blachę formułek bez zrozumienia co robią i do czego służą.
Tym czasem matematyka to sztuka upraszczania rzeczywistości, i rozwiązywania problemów.
Jest to łączenie kilku znanych faktów, żeby dostać rozwiązanie trapiącego nas problemu.
Matematyka to nie jest tylko liczenie cosinusów. Matematyką jest też prowadzenie śledztwa, gdzie na podstawie kilku poszlak dedukujemy jaki był przebieg zdarzeń (ofiara ma w ciele rany kłute. Czyli napastnik się musiał zbliżyć, a ofiara nie uciekła. Być może napastnik znał się z ofiarą?).
Większość sytuacji w codziennym życiu jest przewidywalna. Znając godzinę wyjścia z domu, możemy przewidzieć czy zdążymy na autobus. Mając poprzednie doświadczenia, możemy przewidzieć co się stanie w podobnej sytuacji, tak jak możemy przewidzieć co się stanie jeżeli dotkniemy gołą ręką rozgrzanej patelni.
Liczby, nierówności, i równania są jedynie abstrakcyjną, uproszczoną rzeczywistością. Jeżeli chcemy się dowiedzieć ile wynosi przekątna naszego monitora, to przy obliczaniu tego rozważamy trójkąt prostokątny, twierdzenie pitagorasa, i tym podobne obiekty, a nie monitor LG 24MR400‑B
Całki, sumy, granice, pochodne, pochodne wyższych rzędów... Wszystkie z tych obiektów obserwujemy na codzień, nie będąc tego w ogóle świadomym. Z jaką prędkością porusza się nasz samochód? Z prędkością równą pochodnej przebytej drogi w tym czasie. Jaką trasę pokona nasz samochód jadąc z zadaną prędkością? Pokona trasę równą całce z prędkości.
Te abstrakcyjne matematyczne konstrukcje nie istnieją w prawdziwym życiu (Czy ktoś kiedyś widział dziką trójke, funkcję wykładniczą, albo graniastosłup prawidłowy?), a jednak posiadają odpowiedzi na prawie wszystkie pytania jakie możemy zadać na codzień. Konstrukcja jest jedynie reprezentowana w liczbach, ale tak na prawdę jest to uniwersalny zestaw reguł który zadziała tak samo w każdych warunkach, przy każdej mającej sens reprezentacji.
Dla niektórych, na obrazku widzimy losowo pokolorowany arkusz z excela.
Dla mnie, jest tu zakodowana odpowiedź czym zainteresuję klienta
#gownowpis

Matematyka jest interesująca nawet dla ludzi bez autyzmu...ale w pewnym powiedzmy normalnym stopniu XD
są różne zboczenia
Jak ja Cię rozumiem, piąteczka!
Zaloguj się aby komentować
tez was uczyli w szkole że cyfra to liczba całkowita od 0 do 9? #szkola #matematyka
@hapaczuri Standardowo - najpierw niepoprawne uproszczenie, później ewentualnie nauczysz się mniej niepoprawnego uproszczenia a potem ewentualnie na końcu poznasz prawdę
W każdej chyba dziedzinie tak jest.
W sumie ciekawa rozkmina. Czy rzymskie IV to cyfra, czy dwie cyfry, I i V? A w systemie szesnastkowym, f to też cyfra? xd
No ja wiem, że jest np. liczba dwucyfrowa, ale nie ma cyfry dwuliczbowej
Zaloguj się aby komentować
Chwile mi zajelo, zeby to zrozumiec, ale ma to genialny sens. Nigdy w tym tysiacleciu bym na to nie wpadl.
#matematyka #ciekawostki#prawdopodobienstwo
@bartek555 będąc upierdliwym, jakie będzie prawdopodobieństwo, że prowadzący chce użyć tego paradoksu przeciwko graczowi by on nie wygrał? Xd
Chciałem właśnie pisać, że film 21 o tym mówił, ale jest nawet wstawka z niego. Polecam, fajny.
Wyniki IQ 200+ nie mają żadnego sensu, księga rekordów Guinnessa wywaliła już zupełnie tę kategorię. Przez to, że IQ jest tak popularne w popkulturze ludzie zaczęli stosować takie wyniki jak branding czy materiał do budowania swoich mitów.
Najlepszy przykład to Chris Langan. Gość, który nie potrafił zaliczyć szkoły średniej, a sam siebie nazywa najinteligentniejszym człowiekiem świata. Kilka razy podchodził pod fałszywymi nazwiskami do testu "zgodnego z testami IQ", testu, którego się nie powtarza, bo całkowicie zaburza to wynik. Arbitralnie przeliczył sobie najwyższy zdobyty wynik na IQ "ponad 200".
Publikuje w necie swoje para-religijne rozkminy nazywając je "teorią wszystkiego" i mówi jaki to świat nauki jest skorumpowany i zepsuty, bo nie uznaje jego geniuszu. Nie zdziwi was pewnie, że jest jednym z autorytetów amerykańskiej prawicy.
Zaloguj się aby komentować
Ten fakt wywołuje oburzenie u wielu ludzi, zobaczmy co się stanie tutaj xD
0,(9) = 1
Tam jest "równa się", a nie "w przybliżeniu"
#matematyka #ciekawostki
@Vakarian Ale to jest poprawny wynik, w czym problem?
0,(9) = 9 * 0,(1) = 9 * 1/9 = 1
Zaloguj się aby komentować
Praktcznie z każdą liczbą to działa, najłatwiej sprawdzić podstawiając 9 za 2
Zaloguj się aby komentować
@PanNiepoprawny Jakiś podszywany ten matematyk, prawdziwy powiedziałby tu że ma 2 dziewczyny
Zaloguj się aby komentować
@razALgul

Zaloguj się aby komentować
Dla tych co lubią numerki (hehehe)
#matematyka #nauczanie #edukacja no i #kalkazreddita

Już po nas!
@Arkil wiedziałem, czułem w kościach że coś mi się w tej liczbie podoba.
Ale taguj #numerologia
Zaloguj się aby komentować
#heheszki #humorobrazkowy #memy #matematyka #zajebanezfacebooka
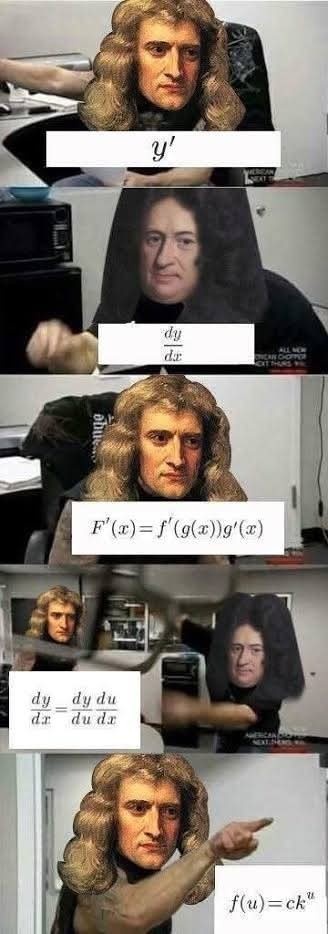
@bori Leibniz>Newton i nawet z tym nie dyskutujcie. Ten brytyjski zjeb przeforsował swoją rację w brytyjskim komitecie, w którym sam zasiadał (i chyba był przewodniczącym?) razem ze swoimi kolegami.
J⁎⁎ać tego fanatyka.
@maximilianan Newton jest królem matematyki jak szczupak jest królem wód.
@bori Leibniz to by Newtonowi łeb upierdolił jednym człapnieciem
Zaloguj się aby komentować
Właśnie dowiedziałem się z Bankiera, że "Po raz pierwszy od 1936 r. będziemy mieć do czynienia z sytuacją, w której, liczba roku jest kwadratem liczby całkowitej. 2025 jest kwadratem liczby 45, kwadrat liczby 46 wypadnie dopiero w 2116 r"
szkieletor.jpg
#ciekawostki #matematyka #wiadomosciswiat #wiadomoscipolska
Niesamowite.
@Michumi kurła, z tego miejsca chce pozdrowic przyszle pokolenie, ktore takie swieto ominelo, nara przegrywy
@Michumi HL 3 confirmed.
Zaloguj się aby komentować
#fizyka #matematyka #rakiety
Mam model rakiety która wg obliczeń poleci na ~120m w górę.
Hipotetycznie możliwe jest wystrzelenie takiej nie w górę, a w bok (tj. w kierunku prostopadłym do siły grawitacji).
Planeta na równiku obraca się z prędkością ~463m/s a rakieta leci z prędkością ~20m/s czyli leci jakieś 5s.
W tym czasie planeta pokona 2315m.
Czy teoretycznie gdybym wystrzelił rakietę na wschód (na równiku), to poleciałaby znacznie dalej niż gdybym strzelił na zachód? Wiem że ta prędkość ma jakieś znaczenie gdy wystrzeliwujemy rakiety na orbitę, bo chcemy właśnie wykorzystać darmowy boost jakim jest przyspieszenie ziemskie
@redve Nie poleci dalej. Wyobraź sobie że odpalasz tę rakietę w pociągu jadącym ze stałą prędkością. Czy pokonana przez rakietę droga względem pociągu zależy od kierunku w którym ją wystrzelisz?
@odyshon na starcie będą mniejsze lub wieksze opory powietrza w sensie że powietrze opływajace pociąg bedzie stanowić przeszkode lub bedzie pomagać. Wim że różnice minimalne ale bedą w odległości lotu. tak se myślę ale jak tylko skuterem jeżdżę
@odyshon względem pociągu tak. Jeżeli wystrzele ją w kierunku przeciwnym do kierunku jazdy pociągu, to po sekundzie będzie ode mnie dalej niż gdybym ją wystrzelił w przeciwnym kierunku.
Jeżeli pociąg jedzie 30m/s a rakieta 20m/s, to po wystrzeleniu jej w tym samym kierunku który jedzie pociąg to rakieta to będzie leciała do tyłu, ale powoli.
Jeżeli ją wystrzele do tyłu, to poleci dalej.
To jest tak samo jak z pluciem przez okno pociągu. Jeżeli będziesz pluł w złą strone to oplujesz sobie buzie
No są to efekty które uwzględniają się w balistyce, ale to dopiero przy prędkościach ponad kilometra na sekundę i dystansach dziatek kilometrów. Pierwszy chyba Eötvös nad Balatonem te pomiary przeprowadzał przy użyciu czulych grawimetrów

Zaloguj się aby komentować