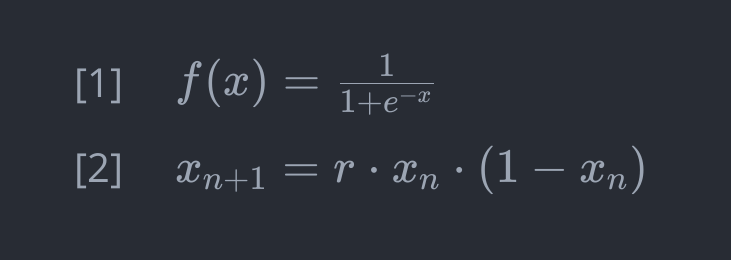Chaos ab ordine - odwzorowanie logistyczne
Z mojej perspektywy ta historia zaczęła się w zamierzchłych czasach, cztery dekady temu. To portal starych ludzi, więc niektórzy z tutejszych bywalców spędzali wtedy czas na rzucaniu kamieniami w brontozaury pod czujnym i pamiętliwym okiem przyszłej premier Kopacz, inni próbowali ujeżdżać welociraptory, jeszcze inni łowili amonity. A ja? Wrzaski latających pterodaktyli mnie przerażały, więc czytałem sobie przy tłuszczowym kaganku magiczne znaki wydrapane na łupkowych płytach.
Jedną z książek, które straszliwie mnie wtenczas skrzywiły i spowodowały, że już nigdy nie spojrzałem na matematykę tak, jak przedtem, była ta o temacie dzisiejszej opowieści.
Wszystko zaczyna się niewinnie. Od pytania o to, jak opisać rozwój populacji. W XIX wieku belgijski matematyk Pierre François Verhulst próbował zrozumieć, jak rzeczywiście rosną populacje w świecie ograniczonych zasobów. Zauważył, że modele wykładniczego (eksponencjalnego) wzrostu, choć eleganckie matematycznie, nie odzwierciedlają rzeczywistości – żadna populacja nie może rosnąć w nieskończoność. Wpadł on wtedy na pewien pomysł - wprowadził do równania "hamulec" w postaci czynnika konkurencji. Gdy populacja jest mała, może się rozwijać niemal swobodnie, ale gdy zbliża się do pojemności środowiska, wzrost zwalnia. Równanie [1] (równania zamieszczam na pierwszym obrazku, bo nie mogę ich wpisać w edytorze w LaTeX jak normalny człowiek, tylko muszę kombinować).
Wiele lat później, w latach siedemdziesiątych XX wieku biolog Robert May przekształcił tę ideę w dyskretne odwzorowanie, które dzisiaj znamy jako odwzorowanie logistyczne - równanie [2]. Dla niewtajemniczonych, "dyskretne" w matematyce nie oznacza czegoś nie rzucającego się w oczy - oznacza zaś proces nieciągły, krokowy, którego następny krok zależy od poprzedniego. Tak, jak w równaniu [2] gdzie lewa strona to stan krok dalej od prawej. Matematyka dyskretna to cały zestaw działów matematyki zajmujących się procesami opartymi o zbiory przeliczalne. Nie będę wnikał głębiej, ale dość wiedzieć, że te maszyny, którymi się posługujemy, smartfony, komputery, działają właśnie dzięki zasadom określonym przez matematykę dyskretną.
Wracając jednak do wzoru Maya - zmienna x w kroku poprzedzającym reprezentuje populację w danym momencie (jako ułamek maksymalnej możliwej, arbitralnie przyjętej populacji), r to parametr wzrostu – kombinacja współczynnika urodzeń i śmiertelności. Gdy r jest małe, populacja po prostu wymiera. Gdy jest większe, ale nie za duże, ustala się na stabilnym poziomie. Ale gdy r przekracza pewne magiczne wartości... wtedy zaczyna się jazda.
Anatomia chaosu
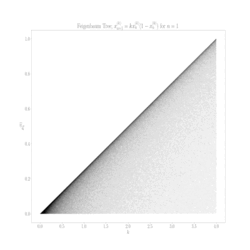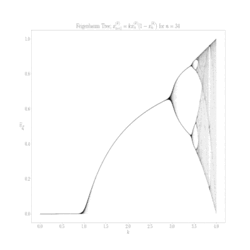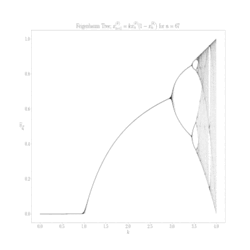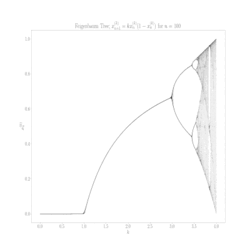
Aby zrozumieć, co się dzieje, stwórzmy sobie diagram bifurkacyjny (drugi obrazek) – odwzorowanie logistyczne, które pokazuje długoterminowe zachowanie systemu w zależności od parametru r. Proces tworzenia takiego diagramu jest prosty: dla każdej wartości r startujemy z dowolną populacją początkową, iterujemy (powtarzamy krok po kroku) równanie setki razy, czekamy aż system się "ustabilizuje", a potem rysujemy punkty reprezentujące wartości, które nam z równania wyszły.
Na początku, gdy r jest mniejsze od 1, widzimy pustą przestrzeń – populacja po prostu wymiera i dąży do 0. Gdy r przekracza 1, pojawia się pojedyncza linia reprezentująca stabilny punkt stały. System znalazł swoją równowagę. Ale przy r równym 3 dzieje się coś nieoczekiwanego – linia się rozdziela.
To pierwszy moment zaskoczenia: bifurkacja (czyli rozdzielenie - tylko tak mądrzej). System nie może już zdecydować się na jedną wartość i zaczyna oscylować między dwoma. Jeszcze nic niezwykłego, równania mogą mieć więcej, niż jedno rozwiązanie, to wiemy ze szkoły, choć fakt, że populacja rośnie i maleje w regularnym cyklu, jakby nie mogła znaleźć sobie miejsca jest nieco niepokojący. Ale to dopiero początek.
Gdy r rośnie dalej, następuje kolejna bifurkacja przy około 3.45. Dwie linie stają się czterema – system oscyluje teraz między czterema wartościami. Potem przy około 3.54 mamy osiem wartości, przy 3.56 szesnaście, i tak dalej. To jest słynna kaskada podwajania okresu – jeden z najciekawszych przykładów drogi do chaosu.
Próg 3.57
W okolicach r = 3.56995 dzieje się coś naprawdę dramatycznego. Regularne wzorce nagle znikają, zastąpione przez pozornie przypadkowe zachowanie. To jest próg chaosu – moment, w którym system traci wszelką przewidywalność w długiej perspektywie. Populacja skacze chaotycznie, nigdy nie powtarzając dokładnie tego samego wzorca.
Ale chaos nie oznacza całkowitego braku struktury. Gdy patrzymy na gęstość punktów w chaotycznym reżimie, odkrywamy, że mają one określony rozkład. Dla r = 4 ten rozkład można nawet dokładnie obliczyć matematycznie – to krzywa w kształcie odwróconej litery U, która pokazuje, że niektóre wartości populacji są bardziej prawdopodobne niż inne.
Co więcej, system wykazuje właściwość zwaną przejściowością topologiczną. Oznacza to, że można znaleźć warunki początkowe, dla których orbita systemu przejdzie arbitralnie blisko każdego punktu w dozwolonym obszarze. To matematyczny sposób powiedzenia, że chaos jest rzeczywiście wszędzie.
Wyspy stabilności
Jednym z najbardziej zaskakujących odkryć było to, że nawet w chaotycznym reżimie istnieją małe "wyspy stabilności". Około r = 3.83 system nagle wraca do regularnego zachowania, oscylując między trzema wartościami.
Te wyspy nie są przypadkowe. Wynikają z głębokiej twierdzenia Szarkowskiego, które mówi, że jeśli system ma cykl o okresie 3, to może mieć cykle o każdym innym okresie. "Okres 3 implikuje chaos" – to jedna z najsłynniejszych fraz w teorii chaosu.
Samopodobieństwo
Gdy powiększymy diagram bifurkacyjny, odkrywamy jedną z najciekawszych właściwości odwzorowania logistycznego: samopodobieństwo. Małe fragmenty diagramu wyglądają jak pomniejszone kopie całości. To jest typowa cecha fraktali – struktur, które wyglądają podobnie na każdej skali.
Ta samopodobność nie jest przypadkowa. Wynika z praw matematycznych, które zostały odkryte przez fizyka Mitchella Feigenbauma w latach 70. Feigenbaum zauważył, że odstępy między kolejnymi bifurkacjami zmniejszają się w określonym tempie, opisywanym przez uniwersalną stałą delta = 4.669201609... Ta stała, znana dzisiaj jako stała Feigenbauma, pojawia się w zupełnie różnych systemach chaotycznych – od obwodów elektrycznych po reakcje chemiczne. I o niej może kiedy napiszę coś więcej.
Zbiór Cantora
O zbiorze Cantora może się również kiedyś jeszcze rozpiszę, tu będzie tylko wzmianka.
Gdy r przekracza 4, odwzorowanie logistyczne pokazuje swoją prawdziwą, chaotyczną naturę. Większość punktów startowych prowadzi do orbit, które uciekają do nieskończoności. Ale te punkty, które zostają w przedziale od 0 do 1, tworzą niezwykłą strukturę zwaną zbiorem Cantora.
Zbiór Cantora powstaje przez iteracyjne usuwanie środkowych trzecich części z przedziałów. Zaczynamy od odcinka jednostkowego usuwamy środkową jedną trzecią, zostają nam więc dwa odcinki. Z każdego z nich znowu usuwamy środkową trzecią, i tak dalej. W granicy (nieskończoności) otrzymujemy zbiór, który jest nigdzie gęsty (ma "dziury" wszędzie), ale jednocześnie nieprzeliczalny – zawiera więcej punktów niż liczby naturalne.
To jest struktura, w której "żyje" chaos dla r > 4. Chaotyczne orbity mogą ten zbiór eksplorować w nieskończenie skomplikowany sposób.
Związek z Mandelbrotem
Jednym z najpiękniejszych odkryć było to, że odwzorowanie logistyczne jest ściśle związane z najsłynniejszym chyba fraktalem świata – zbiorem Mandelbrota. Przez odpowiednią transformację współrzędnych można pokazać, że iteracja jednego równania jest równoważna iteracji drugiego.
Oznacza to, że główny "korpus" zbioru Mandelbrota zawiera w sobie całą dynamikę odwzorowania logistycznego. Wszystkie te bifurkacje, podwajanie okresu, chaotyczne regiony i wyspy stabilności – wszystko to jest tam, w geometrii zbioru Mandelbrota.
I co dalej?
Dalej jest całe piękno matematyki, groźne, czasem przytłaczające, ale fascynujące. Tutaj tylko liznęliśmy nieco po wierzchu.
Odwzorowanie logistyczne stało się jednym z najważniejszych przykładów w teorii chaosu. Pokazało, że deterministyczne, niby przewidywalne, systemy mogą wykazywać nieprzewidywalne zachowanie, że proste równania mogą generować nieskończenie skomplikowane wzorce, i że chaos ma swoją własną, głęboką strukturę matematyczną.
Matematyka nie jest tylko abstrakcyjną grą, ale językiem, którym natura opisuje swoje tajemnice. A my ten język jedynie odczytujemy, bo, cytując Benoit Mandelbrota: "Chmury nie są kulami, góry nie są stożkami, linie brzegowe nie są okręgami, a kora nie jest gładka, ani błyskawica nie porusza się po linii prostej".
Wpis z wiki po angielsku (lepszy) - https://en.wikipedia.org/wiki/Logistic_map
Wpis z wiki po polsku (marny) - https://pl.wikipedia.org/wiki/Odwzorowanie_logistyczne
Równanie logistyczne (polski) - https://mst.mimuw.edu.pl/lecture.php?lecture=mbm&part=Ch2
#matematyka #nauka #ciekawostki