Zaloguj się aby komentować
Kancelaria Prezydenta uważa, że trzeba rozpocząć prace przygotowawcze do wejścia do Rady Pokoju — powiedział w środę szef prezydenckiego Biura Polityki Międzynarodowej Marcin Przydacz. Dodał, że KPRP chciałaby uzyskać stanowisko rządu w tej sprawie oraz poznać opinie wszystkich ugrupowań sejmowych.
Prezydent USA Donald Trump zainaugurował w styczniu w szwajcarskim Davos powołaną przez siebie Radę Pokoju. Państwa członkowskie mają być wybierane przez Trumpa na trzyletnie kadencje, chyba że zapłacą ponad 1 mld dolarów za stałe członkostwo. Trump ma być dożywotnim prezesem Rady o niemal nieograniczonych uprawnieniach.
Zatem sonda - co o tym sądzicie?
#polityka #radapokoju #politykazagraniczna
Czy Polska powinna przystąpić do Rady Pokoju?
Oczywiście, że powinniśmy pozorować ruchy, że chcemy, że my bardzo lubimy USA, no ale wiecie te złe Tuski i UE utrudniają.
patrzac na to kto tam jest to spory obciach.
polska powinna utworzyc wlasna rade pokoju (with blackjack and hookers) i wpisowe powinno byc 10 ton amunicji dla ukrainy
Zaloguj się aby komentować
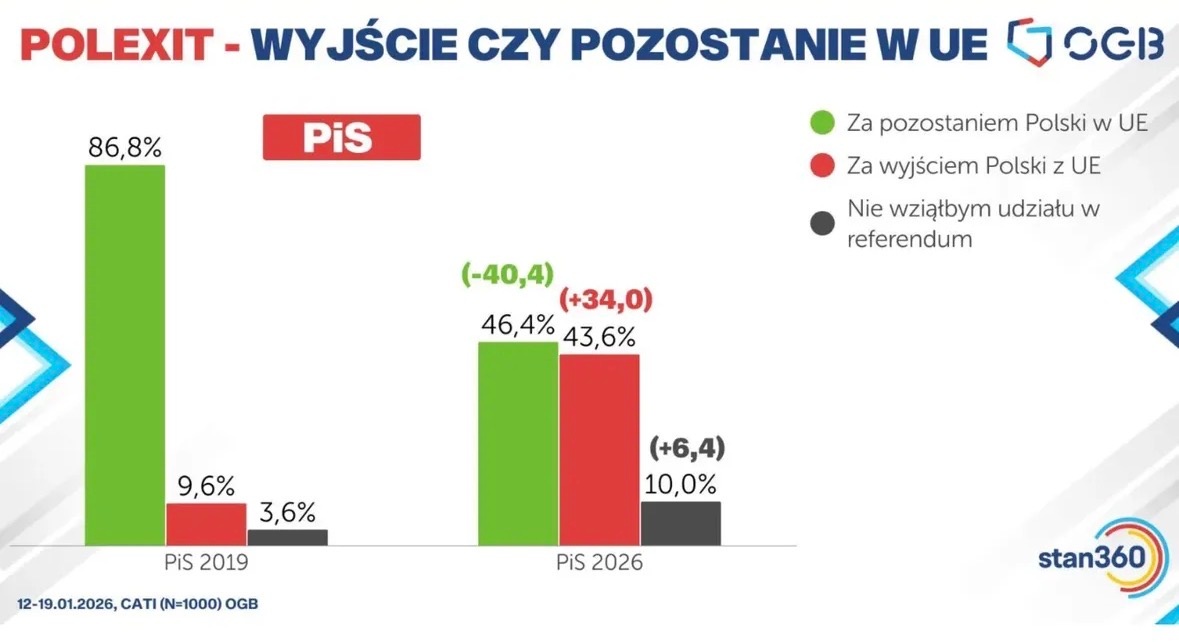
co drugi wyborca pissu za wyjściem z UE
ja jednak jestem za tym żeby to sami pisowcy wyszli z UE a Polskę zostawili w spokoju
#bekazpisu #bekazprawakow #polityka
Myślę że wprowadzenie ETS2 pomoże, ludzie w końcu zobaczą, że ta cała ekologia ma sens oraz że ciepło i mobilność to przywilej bogatych.
Typowe rozumowanie pisowca: -Unia zła!! Polexiti!! Oni chcą nas zniszczyć!! -Ale wiesz,że jak wyjdziemy z Uni to skończą się dopłaty dla rolników,dofinansowania do inwestycji, ogólnie będziemy w czarnej d⁎⁎ie. -Yyyyyyyyyy,,ja nie wiedział ja nie pomyslał.Ale jak to nie będzie dopłat? Unia już nic nie da? H⁎j z tym damy radę!! Polexiti!!!!
@festiwal_otwartego_parasola
>ja jednak jestem za tym żeby to sami pisowcy wyszli z UE a Polskę zostawili w spokoju
A Ci drudzy, każą Ci jechać (z innymi) na zachód i też zostawili Polskę w spokoju.
Jeśli nie widzisz w tym problemu to świadczy o Twojej krótkowzroczności.
Zaloguj się aby komentować
Proszę państwa tak oto w wieku prawie 35 lat, sam bez pomocy żony czy mamy, skorzystałem z czatu z lekarzem rodzinnym i dostałem L4.
Pierwszy raz w życiu będę na L4...
#chorujzhejto #zdrowie

Zaloguj się aby komentować
#technologia #informatyka #systemkaucyjny #windows
#ankieta
Niezależnie od roku wydania, jaki windows byl/jest nejlepszy?
@DungeonFighter Jeśli mam wybierać z tej listy, to XP SP2/SP3. Zabrakło Windows 2000 (nie Millenium), na którego podstawie później powstało XP. Super stabilny system jak na WIndowsa. Z kompatybilnością gier było słabiej, ale Age Of Empires chodziło, i tyle mi wtedy starczało.
Vista i wszystko późniejsze ma wbudowane DRMy i funkcje szpiegowskie, więc traktuję to jak śmietnik. ¯\_(ツ)_/¯
Zaloguj się aby komentować
W jakich czasach byście chcieli żyć i dlaczego? Uwzględniam tylko czasy nowoczesne.
#ankieta #pytanie
W czasach...
Zaloguj się aby komentować
a wy jaką metodą bedziecie się logować?
#heheszki #ksef #jdg

Zaloguj się aby komentować
Taka ciekawostka przyszla mi do glowy do podzielenia sie z wamk.
W wiekszosci firm z mojej branzy istnieje jakis safety observation system. Polega on na zglaszaniu obserwacji zwiazanych z bepieczentwem (no shit sherlock) czyli np. zauwazylem, ze lezy noz i go zabezpieczylem, wymyslilem system do wyciagania pierdow z d⁎⁎y, zatrzymalem kolege ktory napierdalal szlifierka bez okularow, itp, itd.
Podczas projektu klient za najlepsze obserwacje daje nagrody.
Podczas tego projektu, ktory bedzie trwal jeszcze ponad pol roku mozna wygrac KAZDEGO MIESIACA: - iphone 17 pro 256gb - jakies 2 typy dojebanych sluchawek, jedne sony nauszne drugie chyba jakies bose - cos tam jeszcze fajnego
No i teraz ludzie wymyslaja takie glupoty, ze safety officer musi polowe wypierdalac, bo wstyd xD
@jarezz
#barteknamorzu #ciekawostki #marynarz #statki
Zaloguj się aby komentować
Dziś do naszego karmnika zawitał Kopciuszek zwyczajny.
Według Wiki, w północnej Polsce to dość rzadki widok, a tym bardziej zimą. Jednak co odważniejsze osobniki zimują w naszym kraju. Tego samczyka dobrze znamy, bo latem i jesienią dziarsko ćwierka nam za oknem.
Posilał się dziś suszonymi mącznikami, w których rozsmakowały się sikoreczki.
#ptaki #niecodzienneptaki #ptasieciekawostki #birdwatching #dokarmianieptakow





Zaloguj się aby komentować
Takie cóś. Napisałem sobie tekst i miałem zamiar to obrobić jako tło muzyczno-wizualne do #uniwersumhejto i w sumie to jest nadal w tej konwencji, ale troszkę mi się rozwinęło i wyszło coś innego
Może komuś się spodoba. #hejto
Zaloguj się aby komentować
Zaloguj się aby komentować
o 17 pierwsza rozmowa o pracę od 3 lat. stresik jest
#pracbaza
Zaloguj się aby komentować
PYTANIE DO CHŁOPÓW W ZWIĄZKACH
jak często dostajecie komplementy od swoich partnerek, żon, dziewczyn, kochanek, konkubin?
Zastanawia mnie to zwłaszcza w kontekście osób z hejto, które w większości wydają się dość normalni :)
#zwiazki #psychologia #rozkminy
jak często dostajecie komplementy od swoich partnerek, żon, dziewczyn, kochanek, konkubin?
Zaloguj się aby komentować
xDD ten obrazek przypomnial mi sytuacje z gimbazy, jak raz z kolegami siedzielismy u jednego w ogrodzie i spodziewalismy sie wlamania. Obstawilismy caly teren w parach, przy jednym z wejsc na posesje koledzy schowali sie w krzakach z siekiera. Nagle ktos mowi "ej, ale jak ktos serio sie wlamie i go zajebiemy siekiera to bedzie przypal", po chwili namyslu doszlismy do wniosku, ze potencjalnego wlamywacza trzeba bedzie napieprzac po nogach, bo to raczej przezyje i skutecznie go unieszkodliwi xD
Zaloguj się aby komentować
#nostalgia #lata90 #gownowpis #hejto40plus
Syn mnie ostatnio spytał, co zbierałem jako dziecko, bo on zbiera np. karty piłkarskie i komiksy. Przypomniały mi się m.in. karty telefoniczne.
Pamiętam, że biegałem od automatu do automatu i patrzyłem, czy ktoś może zostawił zużytą kartę.

@WatluszPierwszy mam cały klaser w domu rodzinnym
Tak, karty potrafiły się zaciąć i nie dało się ich samodzielnie wyciągnąć, robili to pracownicy techniczni TP tzw. monterzy.
Zaloguj się aby komentować
Wojna
Treść dla dorosłych lub kontrowersyjna
Wojna
Treść dla dorosłych lub kontrowersyjna
Wyglada na to, ze przyszla i na mnie pora, jestem rozpapierduchaczony.
#piorungate #glupiehejtozabawy #heheszki

Zaloguj się aby komentować
Dziś odkryłem w Mercedesie co to jest stosunek przerywany z Bono z U2
XD
Zdarza się też że muzyka się zacina bo auto myśli ze to komunikat obslugi glosowej
#samochody #motoryzacja
Zaloguj się aby komentować
#polska #bekazpodludzi #zima
W Szczecinie od ostatniego pogromu nadal lodowiska wszędzie. Miasto ma wywalone. Przyjechałem w piątek, na podwórku (duże, 300m+ długości, kilkanaście klatek) pingwiny mógłby mieszkać i jeździć na łyżwach. Czytam kwękanie na grupie. Hur dur, miasto nie robi. Za co my podatki płacimy! I normalne żale że do śmietnika nie można dojść, z psem wyjść a starsi ludzie w ogóle się boją wyjść.
Piszę więc że nie ma problemu, biorę busa, jadę kupić piasek i proszę chętnych do sypania, ogarniemy. Chętnych mrowie: sztuk 1. Słownie JEDEN. Okazało się że jednak nie muszę kupować piasku, ziomek ma na busie trzy tony i to z solą od razu.
Nastepnego dnia akcja: Ziomek powoli jedzie, my we dwóch sobie sypiemy. Nie żałowaliśmy zasobów, poszło 2,5 tony. Zrobiliśmy całe podwórku, ścieżki, chodniki,parkingi i co tylko się dało. Godzinka i po sprawie. Można powiedzieć że życie podwórkowe wróciło do normy.
Dzisiaj zaś na grupie rozgorzała afera starych bab pod tytułem "po go sypali, do domu się niesie!!?1" Mam ochotę wziąć lopatę i wy⁎⁎⁎ać jednej z drugą...

Zaloguj się aby komentować