Znalazłem nowe, darmowe gry:
[Epic Games] Sid Meier’s Civilization® VI Platinum Edition (100% off / FREE)
https://store.epicgames.com/en-US/p/sid-meiers-civilization-vi--platinum-edition
#promocjeCzlowiekaCebuli

Społeczność
Znalazłem nowe, darmowe gry:
[Epic Games] Sid Meier’s Civilization® VI Platinum Edition (100% off / FREE)
https://store.epicgames.com/en-US/p/sid-meiers-civilization-vi--platinum-edition
#promocjeCzlowiekaCebuli
Zaloguj się aby komentować
Nowe wydanie newslettera #unknowNews 👇
[#uN] 🌀 Realistyczne fotki z AI, hackowanie słuchawek, bezpieczeństwo dzieci i... tworzenie szczęścia?!
https://mrugalski.pl/nl/wu/iMjP56s3fIIbkDXY2jS892cA
Chcesz dostawać takie prosto na maila? Zapisz się tutaj:
Zaloguj się aby komentować
No dzień dobry. 18 lipca, Międzynarodowy Dzień Nelsona Mandeli. No, i fajnie. A co więcej:
1. W 1362 r. Koło otrzymało prawa miejskie. Gratulujemy temu wielkopolskiemu miastu.
2. W 1418 r. we Wrocławiu wybuchły zamieszki ochrzczone mianem defenestracji wrocławskiej. Ah, kocham to słowo. Znaczy wyoknienie kogoś, czyli wyrzucenie przez okno. Piękna sprawa.
3. W 1900 r. podpisano akt notarialny, na mocy którego społeczeństwo polskie podarowało Henrykowi Sienkiewiczowi dworek w Oblęgorku. Whoa, miło ze strony społeczeństwa. Dostaliście kiedyś coś od społeczności, nawet lokalnej? Nawet za zasługi?
4. W 1325 r. władca Azteków Tenoch założył stolicę państwa – Tenochtitlán. Podobno piękna cywilizacja, pomijając klasyczne ludzkie występki. Za to architektonicznie już się niby nie można było czepiać.
5. W 1925 r. Adolf Hitler opublikował “Mein Kampf”. Będzie się działo, zobaczycie.
Urodzinki ma Vin Diesel, spaniały kierowca rajdowy, aktor, legenda, itp, itd.
Pozdrawiam cieplutko.
#ciekawostki #ciekawostkizdupy
@RogerThat Dostaliście kiedyś coś od społeczności, nawet lokalnej?
Tak. Raz. Wpierdol. Nie polecam.
Nelson Mandela najbardziej znany jest z tego, że żył, kiedy większość społeczeństwa myslala ze nie żyje - to jest tak zwany efekt mandeli albo mandela schrodingera
Komentarz usunięty
Zaloguj się aby komentować
Nornik, który przytula na pocieszenie
Norniki preriowe wykazują się również rodzajem empatii i pocieszają swoich partnerów lub krewniaków, którym przytrafiło się coś nieprzyjemnego. Przeprowadzone eksperymenty wykazały, że jeśli na jakiś czas rozdzielało się blisko związane ze sobą norniki i wystawiało się jednego z nich na stresujące bodźce – to po ponownym połączeniu nornik, który nie doświadczył stresu, szybko próbował pocieszyć i uspokoić tego zestresowanego, przytulając się do niego, przeczesując i czyszcząc mu futerko.
Ponadto, jeśli nornik widział zestresowanego partnera lub krewniaka, ale nie mógł zbliżyć się do niego, żeby go pocieszyć, to on sam również zaczynał się stresować. Zdaniem badaczy, za tego rodzaju zachowania norników preriowych odpowiada działanie oksytocyny, często nazywanej „hormonem przywiązania”.
#ciekawostki #przyroda #natura #zwierzeta #gryzonie #urocze #nauka
tag serii: #7ciekawostekprzyrodniczych

Jak miałem kiedyś myszoskoczki, to gdy zabierałem jednego z klatki, drugi nerwowo tuptał nóżkami 😃
Przeczytałem Normik
Co ciekawe, jeżeli dobrze pamiętam ze studiów ten sam gatunek ale żyjący w innych rejonach, (gdzie występuje izolacja geograficzna między dwoma populacjami), wykazuje mniejsza ilość oksytocyny i ten gatunek już nie wykazuje monogamii. Taki troche poszlaka jak bardzo jesteśmy niewolnikami naszych hormonów
@Cori01 Bardzo ciekawe.
@Cori01 Wniosek taki, zeby szukac empatycznych misiow do zwiazkow, a nie "niegrzecznych chlopakow" o obnizonym poziomie empatii.
Zaloguj się aby komentować
Zdjęcie przedstawia ostatniego konia kopalnianego (nie skamielinę, tylko takiego co pracował w kopalni) po definitywnym zakończeniu wykorzystywania koni w angielskich kopalniach węgla 3 grudnia 1972.
Klacz o imieniu Ruby zobaczyła światło dzienne pierwszy raz od kilkunastu lat.
Konie kopalniane miały ciężki żywot spędzając większość życia w półmroku i ciemności i wykonując ciężką pracę przy ciągnięciu wagoników z węglem. Były jednocześnie bardzo szanowane przez górników jako nieocenieni pomocnicy i towarzysze górniczej niedoli. Konie doskonale wiedziały ile trwa szychta i odmawiały pracy ponad normę.
Dla porównania ostatnie konie "dolne" w polskich kopalniach węgla zakończyły szychtę w 1960 roku, a ostatni koń z kopalni soli w Wieliczce wyjechał wiosną 2002 roku. Konie pracujące na dole miały specjalną dietę, dedykowaną opiekę weterynaryjną oraz normy BHP bardziej restrykcyjne niż ludzie.
#ciekawostki #gornictwo #konie

Tak były szanowane jak te co wożą do morskiego oka
@starszy_mechanik góral to jest inny stan umysłu. To ciężko do człowieka porównać.
Zaloguj się aby komentować
Na początku XIII wieku (czynastego po krakowsku) Cystersi (tacy zakonnicy) opracowali system kodowania cyfr i liczb za pomocą jednego symbolu. System umożliwiał kodowanie dowolnej liczby z zakresu 1-9999 (więcej wtedy nie było potrzebne), a powstał pod wpływem prac uczonego Johna z Basingstoke nad odzwierciedleniem liczb za pomocą kresek wywodzących się ze sposobu reprezentacji liczb przez klasycznych Greków.
System Cystersów był szeroko używany od 13 do 15 wieku do oznaczania i numerowania manuskryptów. Późniejsze odmiany rozszerzające kodowanie do miliona były sporadycznie wykorzystywane w astrologii i numerologii aż do początków 18 wieku.
#ciekawostki #liczby #cystersi

@kitty95 Powinno trafić do Unicode, ale niestety nie trafiło (można to udawać, jakimiś znakami tonalnymi Chao). Na szczęście jest ten font: https://github.com/ctrlcctrlv/FRBCistercian
Sam zapis to, jak wspomniał @matips, zwykły system dziesiętny, tylko w skondensowanej formie.
Myślałem kiedyś, by tak zapisywać hashe na pewnych wydrukach. Ale QR też można mieć w różnych ciekawych wydaniach i jeszcze z korekcją błędów. W tym cysterskim systemie tego brakuje i łatwo o przekłamanie.
@ataxbras qr okiem nie odczytasz.
@kitty95 To prawda, i to był powód moich rozważań, czy nie użyć tego sposobu. Bo jest kompaktowy. Ale wadą jest to, że wytarcie linii powoduje, że 1 może stać się siedem, 4-5, itd. Ten system jest mało odporny na błędy. Już bardziej heksadecymalny, ponieważ dużo trudniej o błąd przy uszkodzeniu wydruku. A czytniki QR są już wszędzie, każdy przy sobie ma smartfon.
Zaloguj się aby komentować
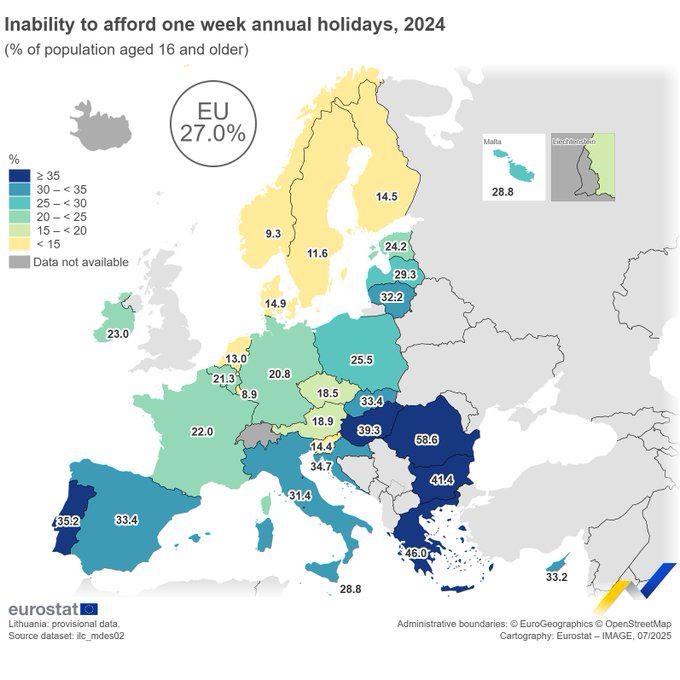
Według badań Eurostatu 25% Polaków powyżej 16r. życia nie jest w stanie pozwolić sobie na tydzień wakacji poza domem. Średnia unijna 27%.
#ciekawostki #polska #europa #podroze #turystyka
Ja w wieku 16lat to moglem sobie pozwolić na paczkę fajek po 6pln i 2 tanie browary.
@Taxidriver fiu, fiu papieroski. Widzę kolega z bogatego domu ( ͡° ͜ʖ ͡°)
@Stashqo w latach 98/99 fajki były tanie jak barszcz.
Paczka L&M kosztowała chyba 4.0-4.50PLN,
Snickers/Mars około złotówki chyba.
Bliżej nam do Niemców i Francuzów niż Hiszpanów czy Włochów (gdzie sobie jeździmy, bo jest tam już niemal... tanio o.O)
Dla mnie OK
Ja bym chciał, żeby mnie było stać na wakacje w Skandynawii, a nie na południu, ale to jeszcze trochę
@mordaJakZiemniaczek sądzę, że ważne by też było wyjaśnienie, co to znaczy “tydzień wakacji”
Tydzień u babci, gdzie się będzie jeździło na rowerze, kapało w lokalnym basenie i jadło na koszt działów (miło wspominam takie wakacje), czy wyjazd grupka do wynajętego domu z basenem w turystycznej okolicy?
@Taxidriver tak, bez sensu określenie. Powinni po prostu mówić ile dane grupy wydają podczas urlopów czy coś. Mogę 10 dni przebiedować w Paryżu za 20e dziennie, bo mam tam szwagra, ale na najtańszy nocleg i rybkę codziennie nad polskim morzem mnie nie stać, jak to ująć w statystyce
@Stashqo przy czym dla polaka to jest biwak z konserwami zabranymi ze sobą, a dla francuza to all inclusive na Maderze
Zaloguj się aby komentować
Dzika matematyka
https://www.youtube.com/watch?v=sbU_cGZ9B74
Wczoraj, uraczyłem Was tym wpisem o odwzorowaniu logistycznym. Najwidoczniej, #niemraodfizy , Sabina, zgapiła pomysł i opublikowała 10 ciekawostek matematycznych na swoim kanale. Włączając w to odwzorowanie logistyczne.
No plagiat jak nic
Na te matematyczne ciekawostki zakładam tag #dzikamatematyka, żeby można było blokować to nudziarstwo.
#matematyka #nauka #ciekawostki #dzikamatematyka
jestem pierwszym obserwującym
@ataxbras napraw tag panie kolego
@Foofy_Shmoofer A co z nim nie tak?
Sabina wrzuca merytoryczne materiały zrobione na odpierdol, żeby trochę rozrzedzić swoje antynaukowe narzekania.
Bardzo lubiłem ten kanał, ale sądzę, że jest teraz na równi pochyłej w kierunku antynaukowego griftera. Zobaczymy.
@mordaJakZiemniaczek Wybacz, ale to ten dupek, Professor Dave, prezentuje właśnie antynaukowe i ideologiczne podejście. Obejrzałem jego materiał do momentu, jak próbował przyczepić Sabinie wspieranie kontranaukowości amerykańskiej prawej strony i pokazywał flagi ze swastyką. A dalej oglądał nie będę, bo gość jest radykałem na jakiejś tam stronie pojebanego, politycznego spektrum.
Zaloguj się aby komentować
Larawce OZE
https://biznesalert.pl/latawce-lepsze-niz-turbiny-wiatrowe-30-kw-energii-w-godzine/
Jakby nie pomyśleć to czemu nikt wcześniej na to nie wpadł... Jeśli będzie bezawaryjnie działać tak jak piszą to byłby niezły gamechanger dla miejsc z drastyczny niedoborem prądu...
Czyli jakieś bębny, liny, obsługa, zwijanie lin (to oczywiście jest za darmo), 45 sekund... brzmi jak stabilne, bezobsługowe i skalowalne źródło energii.
Zaloguj się aby komentować
Brokatowe przekąski dla karczowników
U nas te gryzonie są objęte jedynie częściową ochroną gatunkową, jednak w niektórych częściach Europy są zagrożone. Jest tak między innymi w Walii, gdzie karczowniki miejscami już niemal zupełnie wyginęły.
Wiosną tego roku dzięki staraniom Initiative for Nature Conservation Cymru rozpoczęto nowatorski projekt, który ma wspomóc działania na rzecz ochrony karczowników w Walii. Polega on na podrzucaniu dziko żyjącym karczownikom przekąsek - kawałków jabłka posypanych jadalnym, niegroźnym dla lokalnej flory i fauny brokatem. Pozostawiane po takich przekąskach brokatowe odchody są łatwo dostrzegalne w terenie, co powinno ułatwić badaczom oszacowanie, jak przemieszczają się walijskie karczowniki i jaki zasięg mają ich terytoria.
#ciekawostki #przyroda #natura #zwierzeta #gryzonie #walia
tag serii: #7ciekawostekprzyrodniczych

Zaloguj się aby komentować
Znalazłem nowe, darmowe gry:
[IndieGala] Space Pilgrim Episode I: Alpha Centauri ( 100% OFF / FREE )
https://freebies.indiegala.com/space-pilgrim-episode-i-alpha-centauri
#promocjeCzlowiekaCebuli
Zaloguj się aby komentować
Widzieliście kiedyś grzyba, który wygląda jak kosmita? Albo grzyba, który wygląda jakby szedł wam wklepać? Dziś przedstawię łobuza, który łączy obie te cechy
Gwiazdosz czteropromienny należy do rzadkiej rodziny gwiazdoszowatych - chyba wszystkie jej gatunki w Polsce są pod ochroną. Charakterystyczne dla tego Gwiazdosza są cztery nóżki które z rozwojem owocnika odchylają się w dół, przez co wygląda jakby chodził. Niewielki, parucentymetrowy. Rozwija się w lasach i zaroślach, często pod świerkami, chętnie na podłożu wapiennym. Owocniki wytwarza od sierpnia do października, pojedynczo lub w małych grupach.
Jest to również najmniejszy zbadany gatunek gwiazdoszów.
#grzyby #fungi





@Ragnarokk te co wygladaja jak kosmonauta to Sławosze ( ͡° ͜ʖ ͡°)
@aerthevist Raz dosłownie napisałem Sławosz zamist Gwiazdosz
@Ragnarokk Trujący?
@SST82 Pewnie nie. Totalnie pod całkowitą ochroną a rzadszy jak uczciwy poltyk, więc to bez znaczenia. Ale zapewne po prostu niejadalny - czysto trujących jest tak naprawdę mniejszość grzybów, większość po prostu smakuje jak buty
Na pierwszym zdjęciu widzę cycek.
Zaloguj się aby komentować
17 lipca:
Ogólnopolski Dzień Tabaki
Światowy Dzień Emoji
Dzień Tatuażu
#nietypoweswieta #kalendarz #ciekawostki #tabaka #emotikony #emoji

O dzień tatuażu! To ja swietuje moją czachą

@kopytakonia fajnie kwiatki
Zaloguj się aby komentować
No dzień dobry. 17 lipca, w Korei Gorszej Dzień Konstytucji. Tam prezydenci wprowadzają stany wojenne, więc widać, jak ją szanują. A co więcej:
1. W Lesotho Urodziny Króla. Hm, na serio mają króla, który ma dziś urodziny. Kraj wielkości Wielkopolski.
2. W 1386 r. w kościele z mostkiem pokutnic we Wrocławiu zawieszono Dzwon Grzesznika. Hmhmhmh. Do jego rozkołysania potrzeba było ponad pół minuty pracy dzwonników.
3. W 1961 r. odkryto Jaskinię Czarną w Tatrach Zachodnich. Oj, jest co zwiedzać. W sensie głęboko jak u twojej starej.
4. W 1917 r. król brytyjski Jerzy V zmienił nazwisko na Windsor. To za jego panowania w 1922 r. Imperium brytyjskie osiągnęło rozmiar 36,6 kk km2, stając się największym imperium w historii ludzkości. Zaraz za Wielką Lechią z V wieku oraz kolonią bakterii na tyle twojej starej.
5. W 1955 r. otwarto w Kalifornii pierwszy Disneyland.
Urodzinki ma dziś legenda kina oraz “najczęściej oglądana gwiazda telewizyjna na świecie” wg Księgi rekordów Guinnessa, David Michael Hasselhoff. Wiadomo, Pamela Anderson. W sensie pamiętamy, a nie, że urodziny.
Pozdrawiam cieplutko.
#ciekawostki #ciekawostkizdupy
@RogerThat
4. Warto dodać że wcześniej nazwisko brytyjskiej rodziny królewskiej brzmiało "Saxe-Coburg and Gotha" a Jerzy V zmienił je na fali antyniemieckich nastrojów wywołanych trwającą właśnie 1 Wojną Światową.
Zaloguj się aby komentować
Chaos ab ordine - odwzorowanie logistyczne
Z mojej perspektywy ta historia zaczęła się w zamierzchłych czasach, cztery dekady temu. To portal starych ludzi, więc niektórzy z tutejszych bywalców spędzali wtedy czas na rzucaniu kamieniami w brontozaury pod czujnym i pamiętliwym okiem przyszłej premier Kopacz, inni próbowali ujeżdżać welociraptory, jeszcze inni łowili amonity. A ja? Wrzaski latających pterodaktyli mnie przerażały, więc czytałem sobie przy tłuszczowym kaganku magiczne znaki wydrapane na łupkowych płytach.
Jedną z książek, które straszliwie mnie wtenczas skrzywiły i spowodowały, że już nigdy nie spojrzałem na matematykę tak, jak przedtem, była ta o temacie dzisiejszej opowieści.
Wszystko zaczyna się niewinnie. Od pytania o to, jak opisać rozwój populacji. W XIX wieku belgijski matematyk Pierre François Verhulst próbował zrozumieć, jak rzeczywiście rosną populacje w świecie ograniczonych zasobów. Zauważył, że modele wykładniczego (eksponencjalnego) wzrostu, choć eleganckie matematycznie, nie odzwierciedlają rzeczywistości – żadna populacja nie może rosnąć w nieskończoność. Wpadł on wtedy na pewien pomysł - wprowadził do równania "hamulec" w postaci czynnika konkurencji. Gdy populacja jest mała, może się rozwijać niemal swobodnie, ale gdy zbliża się do pojemności środowiska, wzrost zwalnia. Równanie [1] (równania zamieszczam na pierwszym obrazku, bo nie mogę ich wpisać w edytorze w LaTeX jak normalny człowiek, tylko muszę kombinować).
Wiele lat później, w latach siedemdziesiątych XX wieku biolog Robert May przekształcił tę ideę w dyskretne odwzorowanie, które dzisiaj znamy jako odwzorowanie logistyczne - równanie [2]. Dla niewtajemniczonych, "dyskretne" w matematyce nie oznacza czegoś nie rzucającego się w oczy - oznacza zaś proces nieciągły, krokowy, którego następny krok zależy od poprzedniego. Tak, jak w równaniu [2] gdzie lewa strona to stan krok dalej od prawej. Matematyka dyskretna to cały zestaw działów matematyki zajmujących się procesami opartymi o zbiory przeliczalne. Nie będę wnikał głębiej, ale dość wiedzieć, że te maszyny, którymi się posługujemy, smartfony, komputery, działają właśnie dzięki zasadom określonym przez matematykę dyskretną.
Wracając jednak do wzoru Maya - zmienna x w kroku poprzedzającym reprezentuje populację w danym momencie (jako ułamek maksymalnej możliwej, arbitralnie przyjętej populacji), r to parametr wzrostu – kombinacja współczynnika urodzeń i śmiertelności. Gdy r jest małe, populacja po prostu wymiera. Gdy jest większe, ale nie za duże, ustala się na stabilnym poziomie. Ale gdy r przekracza pewne magiczne wartości... wtedy zaczyna się jazda.
Anatomia chaosu
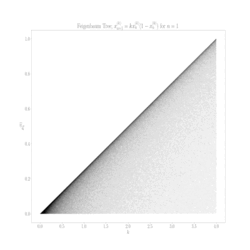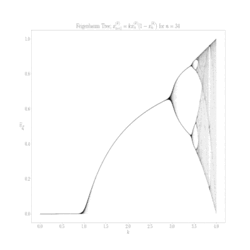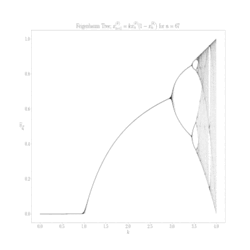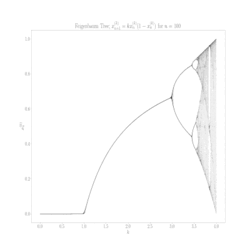
Aby zrozumieć, co się dzieje, stwórzmy sobie diagram bifurkacyjny (drugi obrazek) – odwzorowanie logistyczne, które pokazuje długoterminowe zachowanie systemu w zależności od parametru r. Proces tworzenia takiego diagramu jest prosty: dla każdej wartości r startujemy z dowolną populacją początkową, iterujemy (powtarzamy krok po kroku) równanie setki razy, czekamy aż system się "ustabilizuje", a potem rysujemy punkty reprezentujące wartości, które nam z równania wyszły.
Na początku, gdy r jest mniejsze od 1, widzimy pustą przestrzeń – populacja po prostu wymiera i dąży do 0. Gdy r przekracza 1, pojawia się pojedyncza linia reprezentująca stabilny punkt stały. System znalazł swoją równowagę. Ale przy r równym 3 dzieje się coś nieoczekiwanego – linia się rozdziela.
To pierwszy moment zaskoczenia: bifurkacja (czyli rozdzielenie - tylko tak mądrzej). System nie może już zdecydować się na jedną wartość i zaczyna oscylować między dwoma. Jeszcze nic niezwykłego, równania mogą mieć więcej, niż jedno rozwiązanie, to wiemy ze szkoły, choć fakt, że populacja rośnie i maleje w regularnym cyklu, jakby nie mogła znaleźć sobie miejsca jest nieco niepokojący. Ale to dopiero początek.
Gdy r rośnie dalej, następuje kolejna bifurkacja przy około 3.45. Dwie linie stają się czterema – system oscyluje teraz między czterema wartościami. Potem przy około 3.54 mamy osiem wartości, przy 3.56 szesnaście, i tak dalej. To jest słynna kaskada podwajania okresu – jeden z najciekawszych przykładów drogi do chaosu.
Próg 3.57
W okolicach r = 3.56995 dzieje się coś naprawdę dramatycznego. Regularne wzorce nagle znikają, zastąpione przez pozornie przypadkowe zachowanie. To jest próg chaosu – moment, w którym system traci wszelką przewidywalność w długiej perspektywie. Populacja skacze chaotycznie, nigdy nie powtarzając dokładnie tego samego wzorca.
Ale chaos nie oznacza całkowitego braku struktury. Gdy patrzymy na gęstość punktów w chaotycznym reżimie, odkrywamy, że mają one określony rozkład. Dla r = 4 ten rozkład można nawet dokładnie obliczyć matematycznie – to krzywa w kształcie odwróconej litery U, która pokazuje, że niektóre wartości populacji są bardziej prawdopodobne niż inne.
Co więcej, system wykazuje właściwość zwaną przejściowością topologiczną. Oznacza to, że można znaleźć warunki początkowe, dla których orbita systemu przejdzie arbitralnie blisko każdego punktu w dozwolonym obszarze. To matematyczny sposób powiedzenia, że chaos jest rzeczywiście wszędzie.
Wyspy stabilności
Jednym z najbardziej zaskakujących odkryć było to, że nawet w chaotycznym reżimie istnieją małe "wyspy stabilności". Około r = 3.83 system nagle wraca do regularnego zachowania, oscylując między trzema wartościami.
Te wyspy nie są przypadkowe. Wynikają z głębokiej twierdzenia Szarkowskiego, które mówi, że jeśli system ma cykl o okresie 3, to może mieć cykle o każdym innym okresie. "Okres 3 implikuje chaos" – to jedna z najsłynniejszych fraz w teorii chaosu.
Samopodobieństwo
Gdy powiększymy diagram bifurkacyjny, odkrywamy jedną z najciekawszych właściwości odwzorowania logistycznego: samopodobieństwo. Małe fragmenty diagramu wyglądają jak pomniejszone kopie całości. To jest typowa cecha fraktali – struktur, które wyglądają podobnie na każdej skali.
Ta samopodobność nie jest przypadkowa. Wynika z praw matematycznych, które zostały odkryte przez fizyka Mitchella Feigenbauma w latach 70. Feigenbaum zauważył, że odstępy między kolejnymi bifurkacjami zmniejszają się w określonym tempie, opisywanym przez uniwersalną stałą delta = 4.669201609... Ta stała, znana dzisiaj jako stała Feigenbauma, pojawia się w zupełnie różnych systemach chaotycznych – od obwodów elektrycznych po reakcje chemiczne. I o niej może kiedy napiszę coś więcej.
Zbiór Cantora
O zbiorze Cantora może się również kiedyś jeszcze rozpiszę, tu będzie tylko wzmianka.
Gdy r przekracza 4, odwzorowanie logistyczne pokazuje swoją prawdziwą, chaotyczną naturę. Większość punktów startowych prowadzi do orbit, które uciekają do nieskończoności. Ale te punkty, które zostają w przedziale od 0 do 1, tworzą niezwykłą strukturę zwaną zbiorem Cantora.
Zbiór Cantora powstaje przez iteracyjne usuwanie środkowych trzecich części z przedziałów. Zaczynamy od odcinka jednostkowego usuwamy środkową jedną trzecią, zostają nam więc dwa odcinki. Z każdego z nich znowu usuwamy środkową trzecią, i tak dalej. W granicy (nieskończoności) otrzymujemy zbiór, który jest nigdzie gęsty (ma "dziury" wszędzie), ale jednocześnie nieprzeliczalny – zawiera więcej punktów niż liczby naturalne.
To jest struktura, w której "żyje" chaos dla r > 4. Chaotyczne orbity mogą ten zbiór eksplorować w nieskończenie skomplikowany sposób.
Związek z Mandelbrotem
Jednym z najpiękniejszych odkryć było to, że odwzorowanie logistyczne jest ściśle związane z najsłynniejszym chyba fraktalem świata – zbiorem Mandelbrota. Przez odpowiednią transformację współrzędnych można pokazać, że iteracja jednego równania jest równoważna iteracji drugiego.
Oznacza to, że główny "korpus" zbioru Mandelbrota zawiera w sobie całą dynamikę odwzorowania logistycznego. Wszystkie te bifurkacje, podwajanie okresu, chaotyczne regiony i wyspy stabilności – wszystko to jest tam, w geometrii zbioru Mandelbrota.
I co dalej?
Dalej jest całe piękno matematyki, groźne, czasem przytłaczające, ale fascynujące. Tutaj tylko liznęliśmy nieco po wierzchu.
Odwzorowanie logistyczne stało się jednym z najważniejszych przykładów w teorii chaosu. Pokazało, że deterministyczne, niby przewidywalne, systemy mogą wykazywać nieprzewidywalne zachowanie, że proste równania mogą generować nieskończenie skomplikowane wzorce, i że chaos ma swoją własną, głęboką strukturę matematyczną.
Matematyka nie jest tylko abstrakcyjną grą, ale językiem, którym natura opisuje swoje tajemnice. A my ten język jedynie odczytujemy, bo, cytując Benoit Mandelbrota: "Chmury nie są kulami, góry nie są stożkami, linie brzegowe nie są okręgami, a kora nie jest gładka, ani błyskawica nie porusza się po linii prostej".
Wpis z wiki po angielsku (lepszy) - https://en.wikipedia.org/wiki/Logistic_map
Wpis z wiki po polsku (marny) - https://pl.wikipedia.org/wiki/Odwzorowanie_logistyczne
Równanie logistyczne (polski) - https://mst.mimuw.edu.pl/lecture.php?lecture=mbm&part=Ch2
#matematyka #nauka #ciekawostki
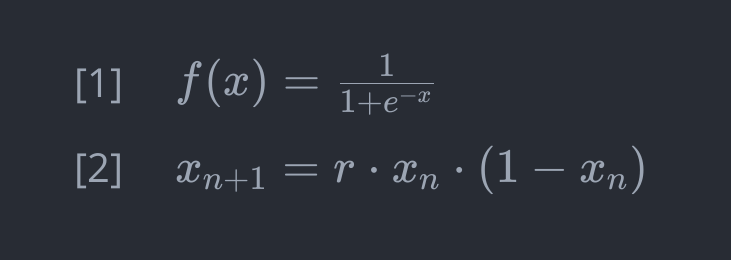
@ataxbras fraktale to widać nawet w drzewach. A tego gifa to dostrzegam w spojrzeniu z góry na linię brzegową gdy są fale. Ostatnio trafiłem na film od Veritasium na YT. Jak dla mnie to na 100% żyjemy w symulacji
@InstytutKonserwacjiMaryliRodowicz Och, za szybko przechodzisz do konkluzji - istnienie fraktali w naturze wynika wprost ze struktury rzeczywistości. Tu każdy stan zależy od poprzedniego. Nic więc dziwnego, że takie struktury się pojawiają. Poczytaj wspomnianego Mandelbrota - The Fractal Geometry of Nature.
Żeby stwierdzić prawdziwość hipotezy symulacji trzeba sporo więcej :D.
@ataxbras będziesz pisał o matematyce więcej to mnie wołaj. Albo taga jakiegoś zrób do śledzenia.
@totengott I zawołam i zrobię tag - może #ciekawostkimatematyczne? Choć to banał. Albo #dzikamatematyka :D. Będzie pod następnym wpisem.
@ataxbras dzięki. #dzikamatematyka Dodane do obserwowanych.
taktyczny komentarz
Zaloguj się aby komentować
Dufrénoyzyt (czarne) - nazwa pochodzi od nazwiska Pierre-Armand Dufrénoya (1792-1857), profesora mineralogii z Paryża.
Realgar (pomarańczowe) - nazwa pochodzi od arab. رهج الغار rahdż al-ghar – „pył (proszek) kopalniany” (z wiki).
To białe to chyba Kwarc.
Fov 4 mm
Fot. z neta
#mineraly

@Wilhelm Arsen jest chyba najbardziej kolorowym pierwiastkiem, w sensie bycia składnikiem wielu minerałów pokrywajacych niemal całą tęczę
Zaloguj się aby komentować
Uroczy szkodnik
Jedna z takich plag miała miejsce w Szkocji w 2011 roku. Populacja norników, przeciętnie licząca tam w przybliżeniu 60 milionów osobników, w ciągu jednego roku urosła do kilkuset milionów - była to najwyższa liczba norników notowana tam od co najmniej dwóch dekad. Podobna plaga nawiedziła w 2007 roku region Kastylii i León w Hiszpanii, powodując poważne szkody w lokalnych uprawach. Szacuje się, że populacja norników wzrosła tam wówczas do co najmniej 700 milionów, wyrządzając szkody w uprawach o powierzchni 500 tysięcy hektarów. Straty oszacowano wówczas na około 15 milionów euro.
Na szczęście dla ludzi, nawet tak niespodziewanie duże "plagi norników" nie przeciągają się poza jeden sezon i do jesieni wygasają. Populacja reguluje się naturalnie, w czym wydatnie pomagają drapieżniki żywiące się nornikami - przede wszystkim ptaki drapieżne, takie jak sowy, myszołowy czy pustułki, dla których lata norniczej plagi to lata obfitości.
Norniki, choć dla ludzi są często szkodnikami, stanowią ważny lub wręcz podstawowy pokarm dla wielu gatunków zwierząt. Ich zupełne zniknięcie spowodowałoby załamanie całych ekosystemów.
#ciekawostki #przyroda #natura #zwierzeta #gryzonie
tag serii: #7ciekawostekprzyrodniczych

Ten uczuć, kiedy opisują cię głównie jako żarcie dla drapieżników.
Zaloguj się aby komentować
Pole siłowe coraz bliżej :D
Tytuł to trochę żart, bo chodzi o odchudzenie osłon ablacyjnych i zastąpienie ich polem magnetycznym (a właściwie indukowaną osłoną elektromagnetyczną). Ten system ma dużą przyszłość, bo płaszcz plazmowy można dodatkowo kształtować, wpływając na właściwości aerodynamiczne.
Zamiast się rozpisywać, notka z Kopalni Wiedzy - https://kopalniawiedzy.pl/pojazd-kosmiczny-atmosfera-pole-magnetyczne-plazma,37986
Dłuższy artykuł - https://news.uq.edu.au/2025-07-uq-conduct-world-first-tests-effectiveness-magnetic-heat-shields-atmospheric-re-entry-large-spacecraft
#nauka #fizyka #ciekawostki
@ataxbras To już jakiś czas temu było o modyfikacji plazmy w trakcie wejścia w atmosferę za pomocą fal radiowych.
@myoniwy Och, badania nad tym trwają od lat sześćdziesiątych. Modyfikować można zarówno komponentem magnetycznym, jak i elektrycznym. Ale wymaga to mocy obliczeniowych, z jednej strony by móc reagować w czasie bliskim rzeczywistego, a z drugiej by móc symulować dynamicznie konieczne zmiany natężeń pól. Stąd precyzyjne sterowanie tym zjawiskiem stało się możliwe dopiero niedawno (to moja działka w pewnym stopniu - zajmowałem się tym od strony właśnie symulacji).
Zaloguj się aby komentować
Dziś 82 lata kończy Pan Tadeusz Sznuk! Wszystkiego najlepszego i przede wszystkim dużo zdrowia!
Pan Tadeusz to pochodzący z Kielc elektronik, który został dziennikarzem radiowym, prezenterem telewizyjnym, lektorem filmowym i pilotem, stał się sławny dzięki prowadzeniu od ponad 30 lat już kultowego teleturnieju Jeden z Dziesięciu. Ma też za sobą nieudany epizod polityczny. W 1989 bez powodzenia kandydował w wyborach do Senatu PRL jako kandydat niezależny w województwie warszawskim, zdobywając 155 tys. głosów.
Jest żonaty i ma dwóch synów i córkę. Żadne z jego dzieci nie poszło w jego ślady. Synowie wybrali zawód informatyka, a córka psychologię społeczną. Jak kiedyś wyjaśnił ma to swoje uzasadnienie: Mieli okazję obserwować tatusia, którego często nie było w domu, więc trzymają się od mediów z daleka. I radio, i latanie człowieka od rodziny oddalają.
#ciekawostki #telewizja #tvp #jedenzdziesieciu

@aerthevist to moje ulubione foto tego Pana

Zaloguj się aby komentować
@Ragnarokk - i po co mnie w to zamieszałeś?
@koszotorobur To dobrze czy źle?
@Ragnarokk - o to, to trzeba zapytać AI
Zaloguj się aby komentować