@owczareknietrzymryjski nie, to stara rozkmina, która w sumie mi się podoba. Tzn w świecie SW było takie pozdro dla kumatych, kto ma super szybki statek ten wie o co chodzi

@mordaJakZiemniaczek super. Ja o czym innym ale ok

@maximilianan zewnętrzny, odległy obserwator będzie widział poprawną drogę i poprawny czas.

Dylatacja czasu i drogi jest tylko lokalnie na statku, która to i tak wyjdzie "na zero" bo to co zyskają podróżując w pobliżu czarnej dziury stracą na próbie wydostania się ze studni gwawitacyjnej.

Przyśpieszenie też powoduje dylatację, a przyśpieszenie potrzebne na ucieczkę z orbity czarnej dziury będzie zajebiste.

@entropy_ generalnie tu są pomieszane pojęcia. Skoro gromada czarnych dziur to powinno to raczej działać jak proca grawitacyjna.

@maximilianan a taka ciekawostka:

"Proca grawitacyjna" taka jak voyager 1 robił na przykład nie dodaje prędkosci tylko zmienia wektor kierunku. Prędkość przed i po manewrze jest taka sama tylko w inną stronę.

ALE

Ten sam manewr w pobliżu czarnej dziury, jeżeli będziesz dostatecznie blisko i zrobisz jak w interstellar że coś do niej wrzucisz to "ukradniesz" trochę prędkości obrotowej z CD i będziesz się poruszał szybciej kosztem spowolnienia obrotu CD

@entropy_ wektor kierunku? ( ͡° ͜ʖ ͡°) Może przemieszczenia?

Dodatkowo proca polega na częściowe zniwelowanie wpływu grawitacji słońca.

@maximilianan no właśnie nie. Zmieniasz kierunek ruchu ale nie prędkość.

Cały myk polega na tym, że używając grawiatacji planety skręcasz w kierunku jaki Ci się podoba bez użycia paliwa. Za darmo.

Dlatego voyager 1 zamiast wejść na orbitę w okół słońca na wysokości jowisza, wykorzystał jowisza żeby prędkość kątową w okół słońca zamienić na taką samą prędkość ale w kierunku ucieczki od słońca.

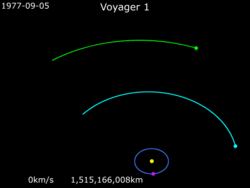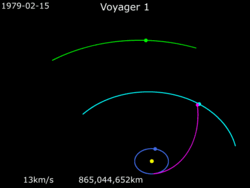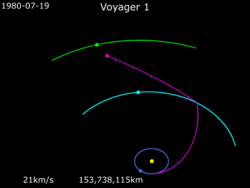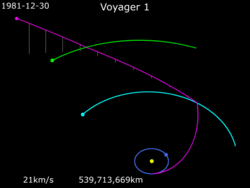
@maximilianan albo inaczej: ta proca zmienia układ odniesienia z prędkości orbitalnej na prędkość względem słońca

@entropy_ @maximilianan Tacy mądrzy jesteście to obliczcie 2 prędkość kosmiczną dla czarnej dziury o masie 100 mas Słońca xD

@bori Ale to zależy w jakiej odległości od czarnej dziury. Jeżeli z "powierzchni" czyli z horyzontu zdarzeń to nie ma co liczyć.

Prędkość ucieczki = prędkość światła.

@entropy_ @maximilianan rozwalają mnie te zajadłe awantury o kompletnie zmyślone bajeczki.

@Opornik A ja lubię jako ćwiczenie dowieść lub kompletnie wykluczyć jakąś idiotyczną sytuację tak jak w przypadku mema podawanie odległości jako jednostki czasu.

@bori Tylko żeby się nie pomylili!

@entropy_ Panie, my tu dyskutujemy kulturalnie o zależności zbliżenia się a prędkością, a Ty od razu z horyzontem zdarzeń wyskakujesz! Co za osobliwość! xD

@entropy_ apropo wpisu z obrazkem z voyagera:

Nie wiem dlaczego wprowadzamy tutaj prędkość kątową, skoro absolutna (kartezjańska względem słońca) jest w tych dywagacjach istotna

Nie zmienia się "prędkość kątowa" tylko względem Jowisza, "absolutnia" zmienia się jak najbardziej, nawet na GIFie to widać

https://pl.wikipedia.org/wiki/Asysta_grawitacyjna?wprov=sfla1

@bori jasne. W którym miejscu dokładnie? Horyzont zdarzeń takiej dziury jest większy niż nasz układ planetarny

@maximilianan Dla ułatwienia obliczeń pomiń opory powietrza