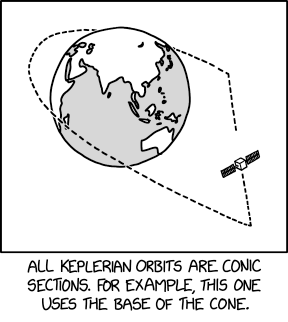
Orbity keplerowskie są przekrojami stożka (a w przypadkach zamkniętych oczywiście elipsami)
Dałem #heheszki i z obrazka chyba widać czemu
Ale poza beką, to dosyć ciekawa i nieco głębsza historia z dodatkowymi ciekawostkami. Tutaj jest nieco szczegółowiej: https://math.ucr.edu/home/baez/gravitational.html .
Keplerowskie orbity zamknięte są sekcjami stożka z powodu prawa odwróconego kwadratu. Ale co mniej oczywiste, orbity takie mają symetrię SO(4) - czyli cztero, a nie trójwymiarową. A wynika to z tego, że prawo odwróconego kwadratu ma więcej symetrii, niż przestrzeń, w której się je stosuje. Sama grupa ma de facto 6 stopni swoboody, symetrii (można rzec, że wymiarów), ale jest opisywalna w 4 wymiarach, bo dodaje jedynie wektor pędu. Wiem, że nie chcialiście tego wiedzieć, ale nie dałem Wam wyboru
https://xkcd.com/3189/
#okazjonalnexkcd #matematyka #fizyka #nauka #ciekawostki #heheszki